Overview

Teaching: 60 min
Exercises: 30 min

Questions

• How can I explore my data by visualization in R?

Objectives

• To be able to use ggplot2 to visuzlize your data

• To understand the basic grammar of graphics, including the aesthetics and geometry layers, adding statistics, transforming scales, and coloring or panelling by groups.

Data visualization

Introduction

“The simple graph has brought more information to the data analyst’s mind than any other device.” — John Tukey

In this lesson we will learn how to visualize your data using ggplot2. R has several systems for making graphs, but ggplot2 is probably the most versatile. ggplot2 implements the grammar of graphics, a coherent system for describing and building graphs. With ggplot2, you can do more faster by learning one system and applying it in many places.

The lesson is based on Chapter 8 of the Bioinformatics Data Skills book by Vince Buffalo and Chapter 2 of the R for Data Science book by Garrett Grolemund and Hadley Wickham.

Additional Resources

• Download the ggplot2 cheatsheet and keep it handy while you are working with the package.
• See the official ggplot2 page for additional resources (including free books).

Prerequisites

ggplot2 is one of the core members of the tidyverse. So begin by loading it with:

library(tidyverse)
# I assume it is installed by now, but see previous episodes if you get an error message!

Dataset #1

We will again use the dataset Dataset_S1.txt from the paper “The Influence of Recombination on Human Genetic Diversity”.
See the previous lesson for its description.

Let’s read it as a tibble and modify as we did before:

dvst <- read_csv("https://raw.githubusercontent.com/vsbuffalo/bds-files/master/chapter-08-r/Dataset_S1.txt") %>% 
  mutate(diversity = Pi / (10*1000), cent = (start >= 25800000 & end <= 29700000)) %>% 
  rename(percent.GC = `%GC`, total.SNPs = `total SNPs`, total.Bases = `total Bases`, reference.Bases = `reference Bases`)

Exploring Data Visually with ggplot2 I: Scatterplots and Densities

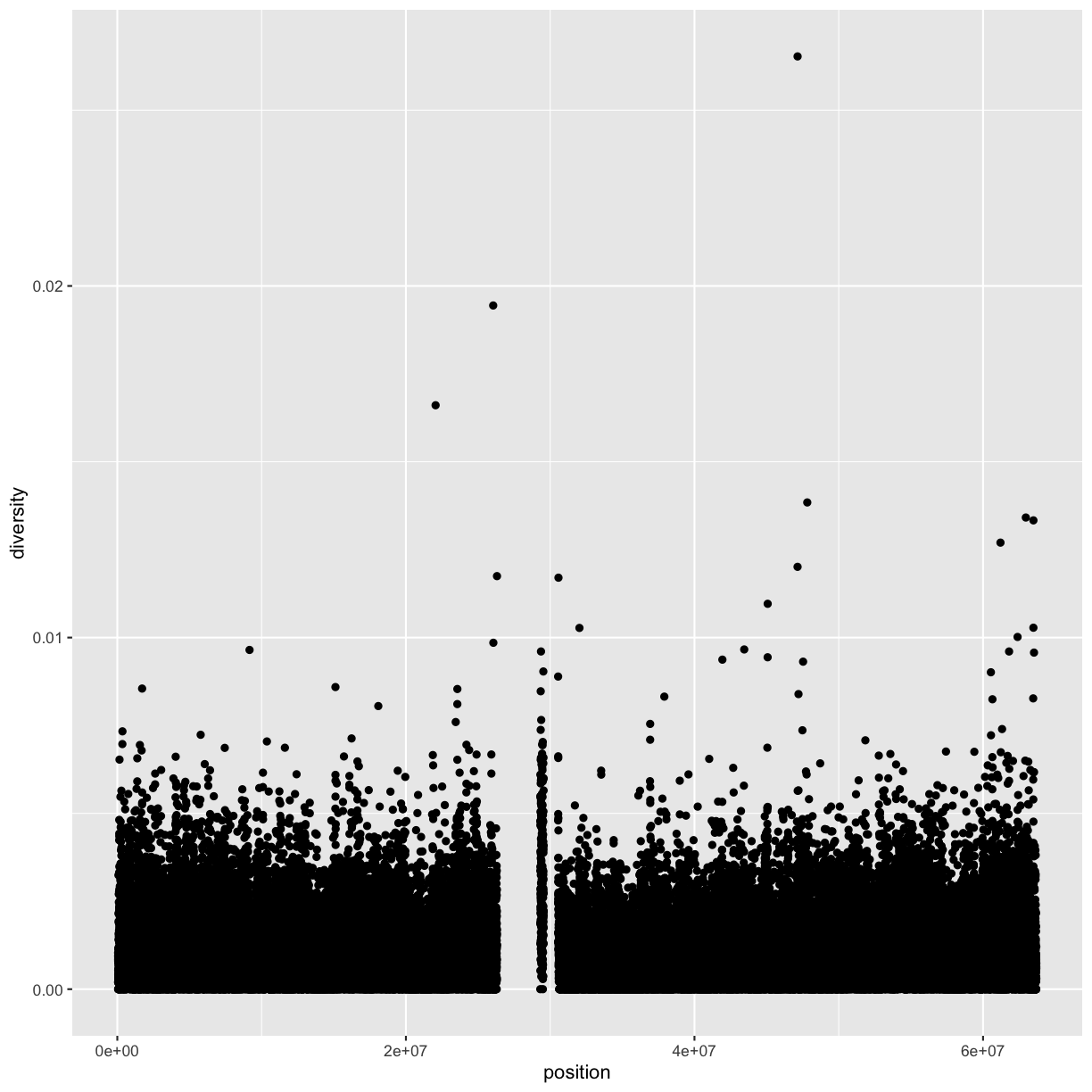
We’ll start by using ggplot2 to create a scatterplot of nucleotide diversity along the chromosome. But because our data is window-based, we’ll first add a column called position that’s the midpoint for each window:

dvst <- mutate(dvst, position = (end + start) / 2)

Now we make a ggplot:

ggplot(data = dvst) + geom_point(mapping=aes(x=position, y=diversity))

Note

With ggplot2, you begin a plot with the function ggplot(). ggplot() creates a coordinate system that you can add layers to. The first argument of ggplot() is the dataset to use in the graph. So ggplot(data = dvrs) creates an empty graph.

You complete your graph by adding one or more layers to ggplot(). geom_point()is a type of geometric object (or geom in ggplot2 lingo) that creates a scatterplot. Note, that to add a layer, we use the same + operator that we use for addition in R.

Each geom function in ggplot2 takes a mapping argument. This defines how variables in your dataset are mapped to visual properties. The mapping argument is always paired with aes(), and the x and y arguments of aes() specify which variables to map to the x and y axes. ggplot2 looks for the mapped variable in the data argument, in this case, dvst.

A graphing template

We can use the code above to make a reusable template for making graphs with ggplot2. To make a graph, replace the bracketed sections in the code below with a dataset, a geom function, or a collection of mappings.

ggplot(data = <DATA>) + 
  <GEOM_FUNCTION>(mapping = aes(<MAPPINGS>))

ggplot2 has many geoms (e.g., geom_line(), geom_bar(), etc). We’ll talk about them later.

Aesthetic mappings

“The greatest value of a picture is when it forces us to notice what we never expected to see.” — John Tukey

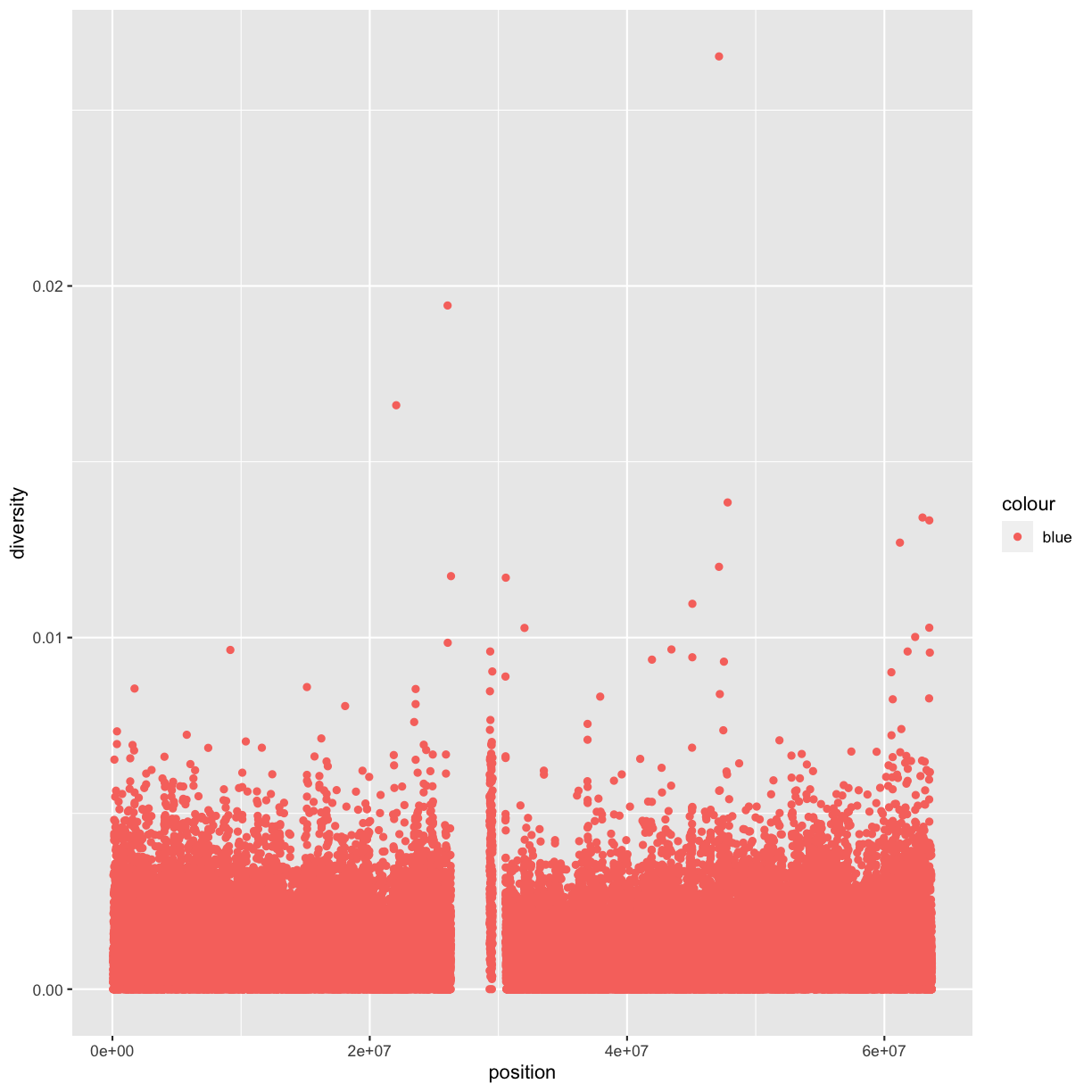
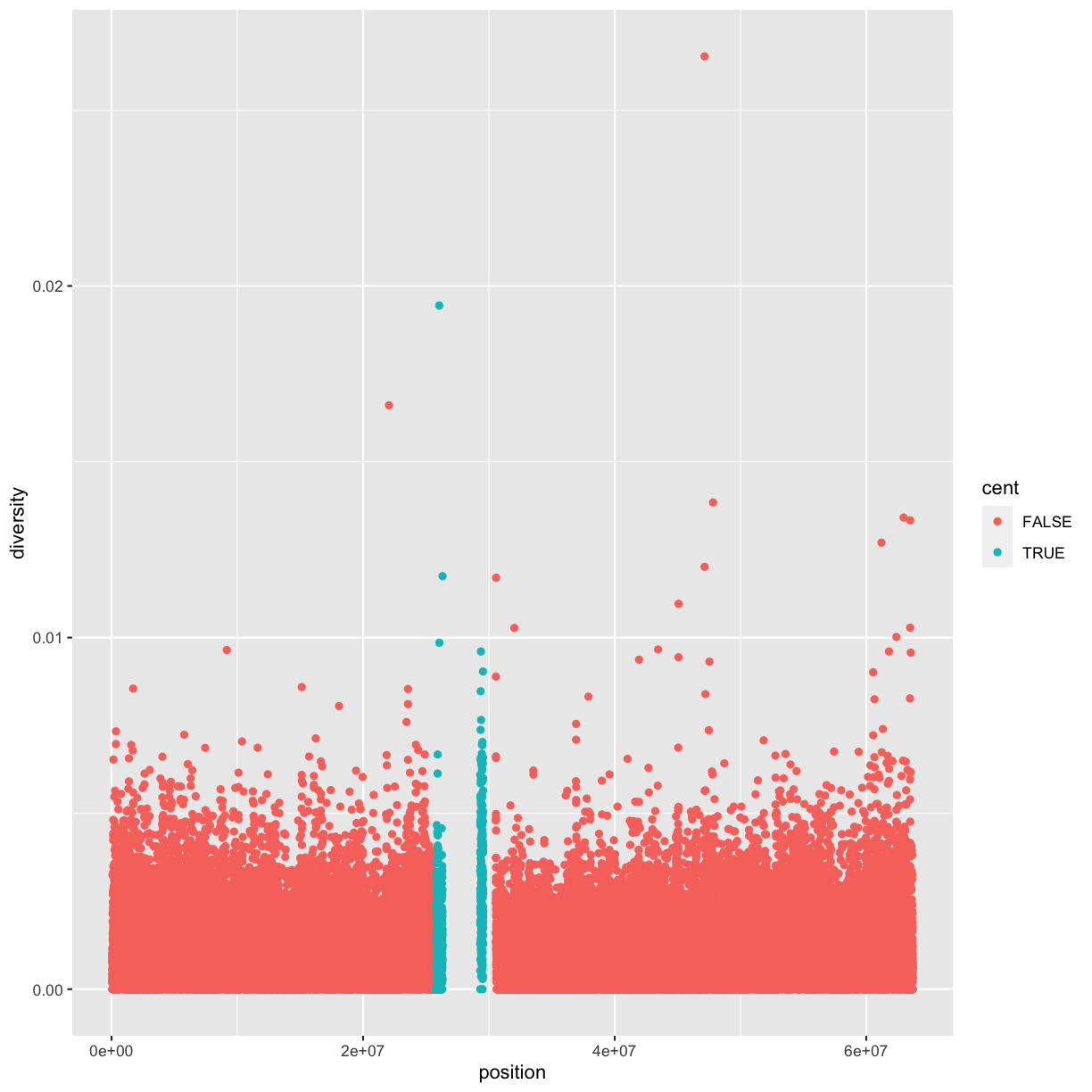
Notice the missing diversity estimates in the middle of this plot. What’s going on in this region? We can explore this question easily in ggplot by mapping a possible confounder or explanatory variable to another aesthetic. In this case, let’s map the color aesthetic of our point geometric objects to the column cent, which indicates whether the window falls in the centromeric region of this chromosome

ggplot(data = dvst) + geom_point(mapping = aes(x=position, y=diversity, color=cent))

Note

Geometric objects have many aesthetic attributes (e.g., color, shape, size, etc.). You can map any of the geometric objects’ aesthetics to columns in your dataframe. The syntax highlights a useful insight about x and y: the x and y locations of a point are themselves aesthetics, visual properties that you can map to variables to display information about the data. Once you map an aesthetic, ggplot2 takes care of the rest. It selects a reasonable scale to use with the aesthetic, and it constructs a legend that explains the mapping between levels and values. For x and y aesthetics, ggplot2 does not create a legend, but it creates an axis line with tick marks and a label. The axis line acts as a legend: it explains the mapping between locations and values.

You can also set the aesthetic properties of your geom manually. For example, we can make all of the points in our plot blue:

ggplot(data = dvst) + 
  geom_point(mapping = aes(x = position, y = diversity), color = "blue")

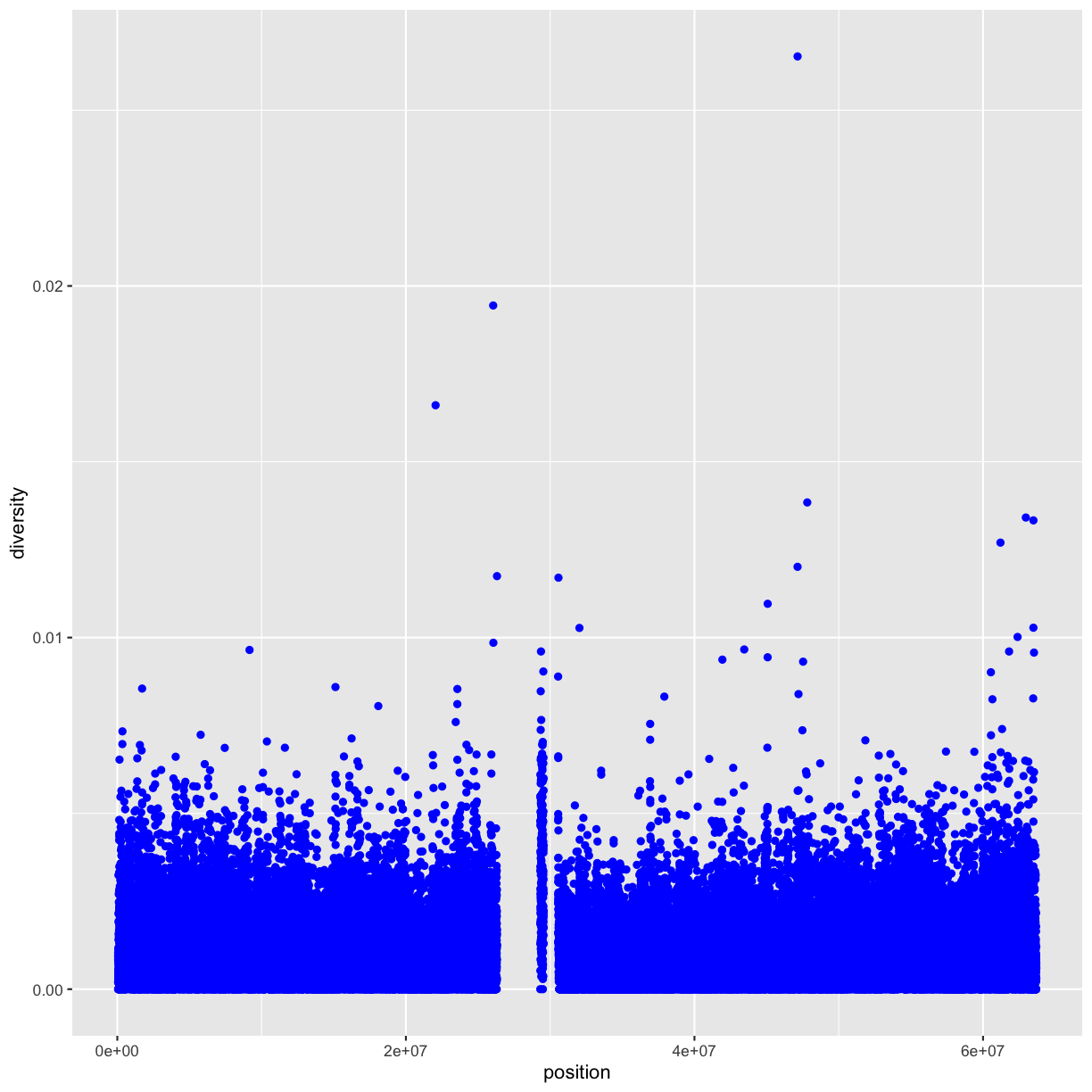
Here, the color doesn’t convey information about a variable, but only changes the appearance of the plot. To set an aesthetic manually, set the aesthetic by name as an argument of your geom function; i.e. it goes outside of aes(). You’ll need to pick a value that makes sense for that aesthetic:

• The name of a color as a character string.
• The size of a point in mm.
• The shape of a point as a number, as shown below.

Finally, note, that aesthetic mappings can also be specified in the call to ggplot(); different geoms will then use this mapping:

ggplot(data = dvst, mapping = (aes(x=position, y=diversity))) + geom_point()

Discussion

1. What’s gone wrong with this code? Why are the points not blue?

   ggplot(data = dvst) + geom_point(mapping = aes(x = position, y = diversity, color = "blue"))
   

   

2. Map a continuous variable to color, size, and shape. How do these aesthetics behave differently for categorical vs. continuous variables?

3. What happens if you map the same variable to multiple aesthetics?

4. What does the stroke aesthetic do? What shapes does it work with? (Hint: use ?geom_point)

5. What happens if you map an aesthetic to something other than a variable name, like aes(colour = percent.GC < 50)?

Common problems

As you start to run R code, you’re likely to run into problems. Don’t worry — it happens to everyone! Here a a few common problems (and solutions):

• Make sure that every ( is matched with a ) and every " is paired with another ".
• Sometimes you’ll run the code and nothing happens. Check the left-hand of your console: if it’s a +, it means that R doesn’t think you’ve typed a complete expression and it’s waiting for you to finish it. In this case, it’s usually easy to start from scratch again by pressing ESCAPE to abort processing the current command.
• One common problem when creating ggplot2 graphics is to put the + in the wrong place: it has to come at the end of the line, not the start. In other words, make sure you haven’t accidentally written code like this:

  ggplot(data = dvst) 
  \+ geom_point(mapping = aes(x = position, y = diversity))
  

Overplotting

One problem with scatterplots (and our plot in particular) is overplotting (some data points obscure the information of other data points). We can’t get a sense of the distribution of diversity from this figure because everything is saturated from about 0.05 and below. One way to alleviate overplotting is to make points somewhat transparent (the transparency level is known as the alpha):

ggplot(data = dvst) + geom_point(mapping = aes(x=position, y=diversity), alpha=0.01)

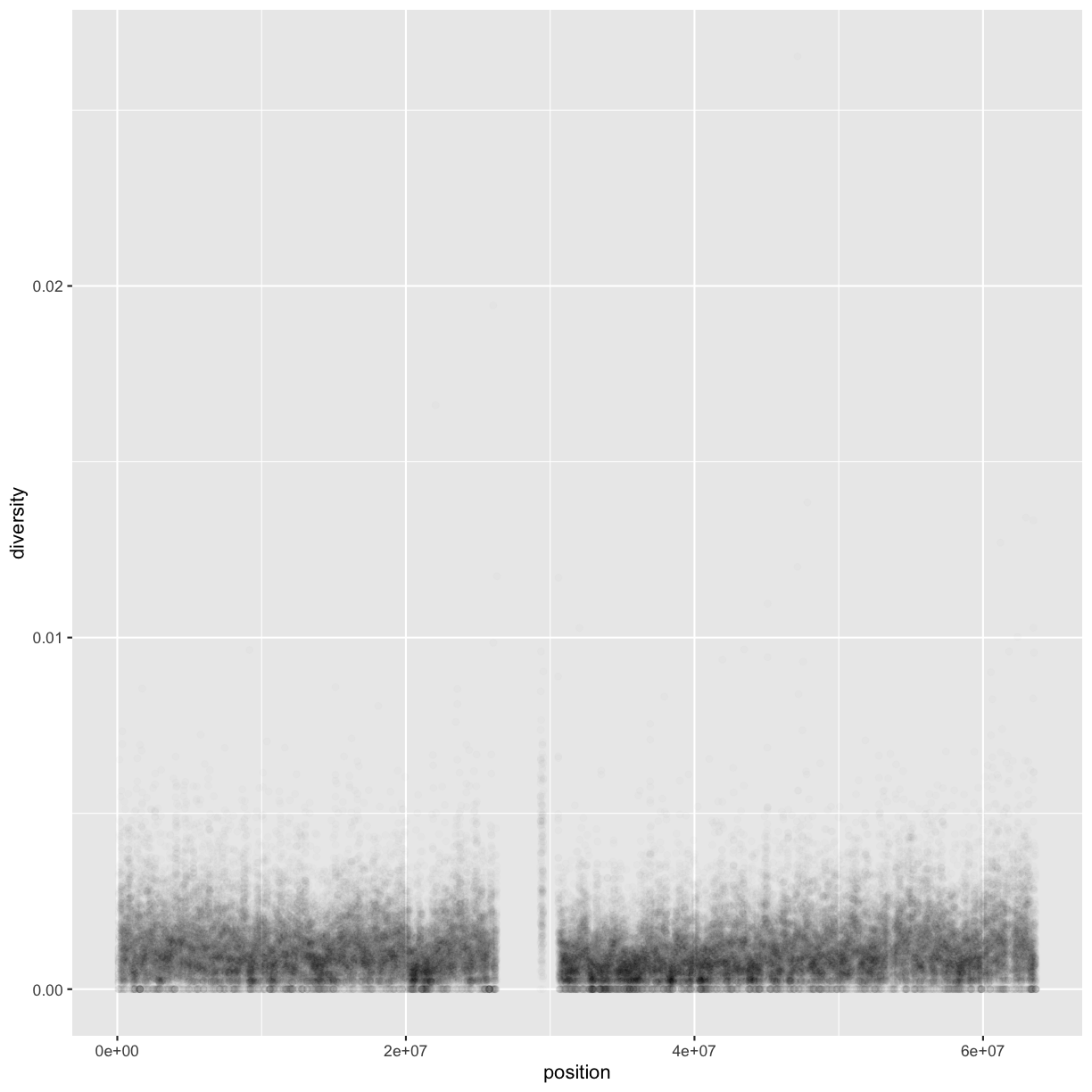Note that we set alpha=0.01 outside of the aesthetic mapping function aes() as we did with the color in the previous example. This is because we’re not mapping the alpha aesthetic to a column of data in our dataframe, but rather givi0ng it a fixed value for all data points.

Density

Let’s now look at the density of diversity across all positions. We’ll use a different geometric object, geom_density(), which is slightly different than geom_point() in that it takes the data and calculates a density from it for us:

ggplot(data = dvst) + geom_density(mapping = aes(x=diversity), fill="blue")

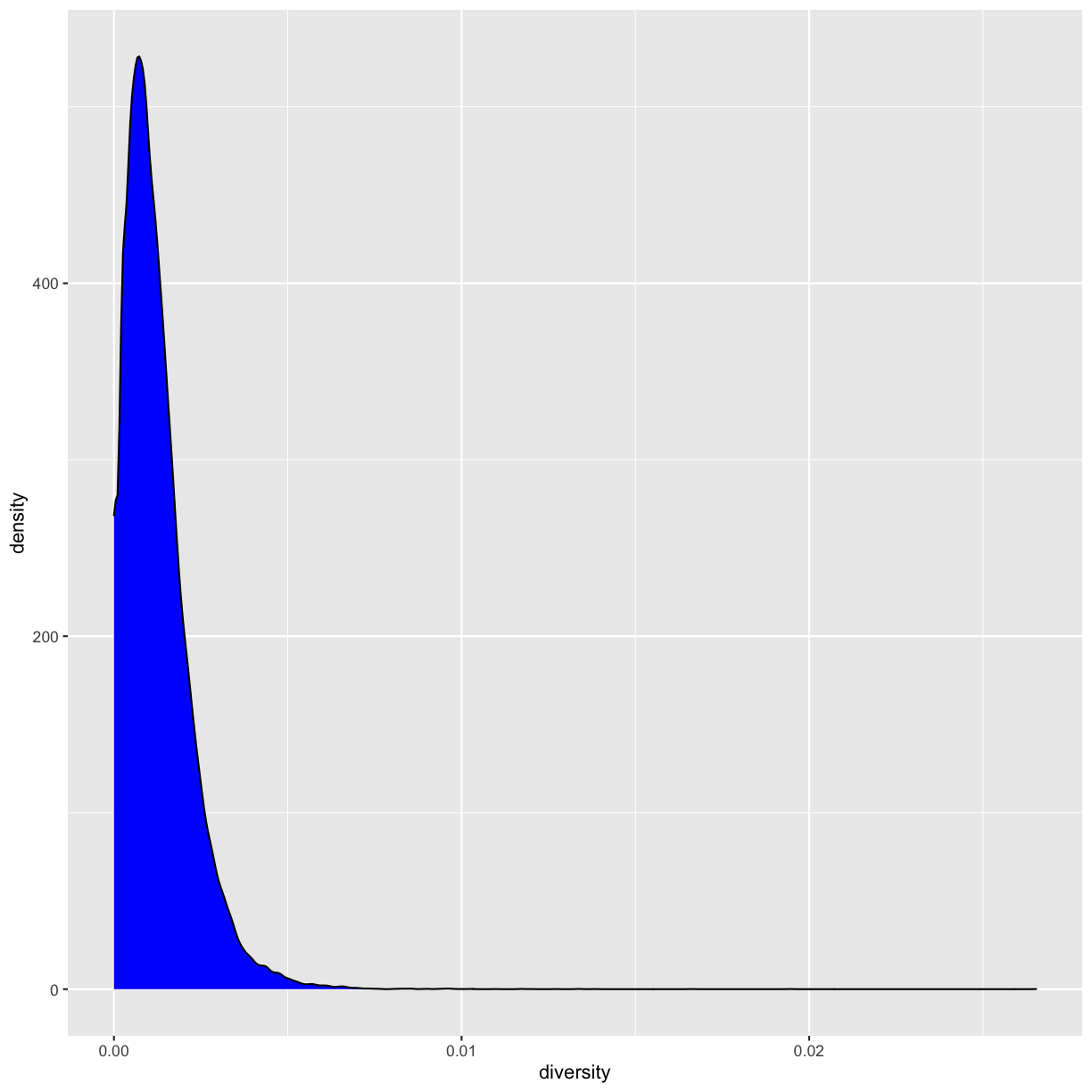
We can also map the color aesthetic of geom_density() to a discrete-valued column in our dataframe, just as we did with geom_point(). geom_density() will create separate density plots, grouping data by the column mapped to the color aesthetic and using colors to indicate the different densities. To see both overlapping densities, we use alpha to set the transparency to 0.4:

ggplot(data = dvst) + geom_density(mapping = aes(x=diversity, fill=cent), alpha=0.4)

Immediately we’re able to see a trend that wasn’t clear by using a scatterplot: diversity is skewed to more extreme values in centromeric regions. Again (because this point is worth repeating), mapping columns to additional aesthetic attributes can reveal patterns and information in the data that may not be apparent in simple plots.

Exploring Data Visually with ggplot2 II: Smoothing

Let’s look at the Dataset_S1.txt data using another useful ggplot2 feature: smoothing. In particular, we’ll investigate potential confounders in genomic data. There are several potential factor that influence our estimates: sequencing read depth; GC content; mapability, or whether a region is capable of having reads correctly align to it; batch effects; etc. Often with large and high-dimension datasets, visualization is the easiest and best way to spot these potential issues.

Earlier, we used transparency to give us a sense of the most dense regions. Another strategy is to use ggplot2’s geom_smooth() to add a smoothing line to plots and look for an unexpected trend. Let’s use a scatterplot and smoothing curve to look at the relationship between the sequencing depth (the depth column) and the total number of SNPs in a window (the total.SNPs column):

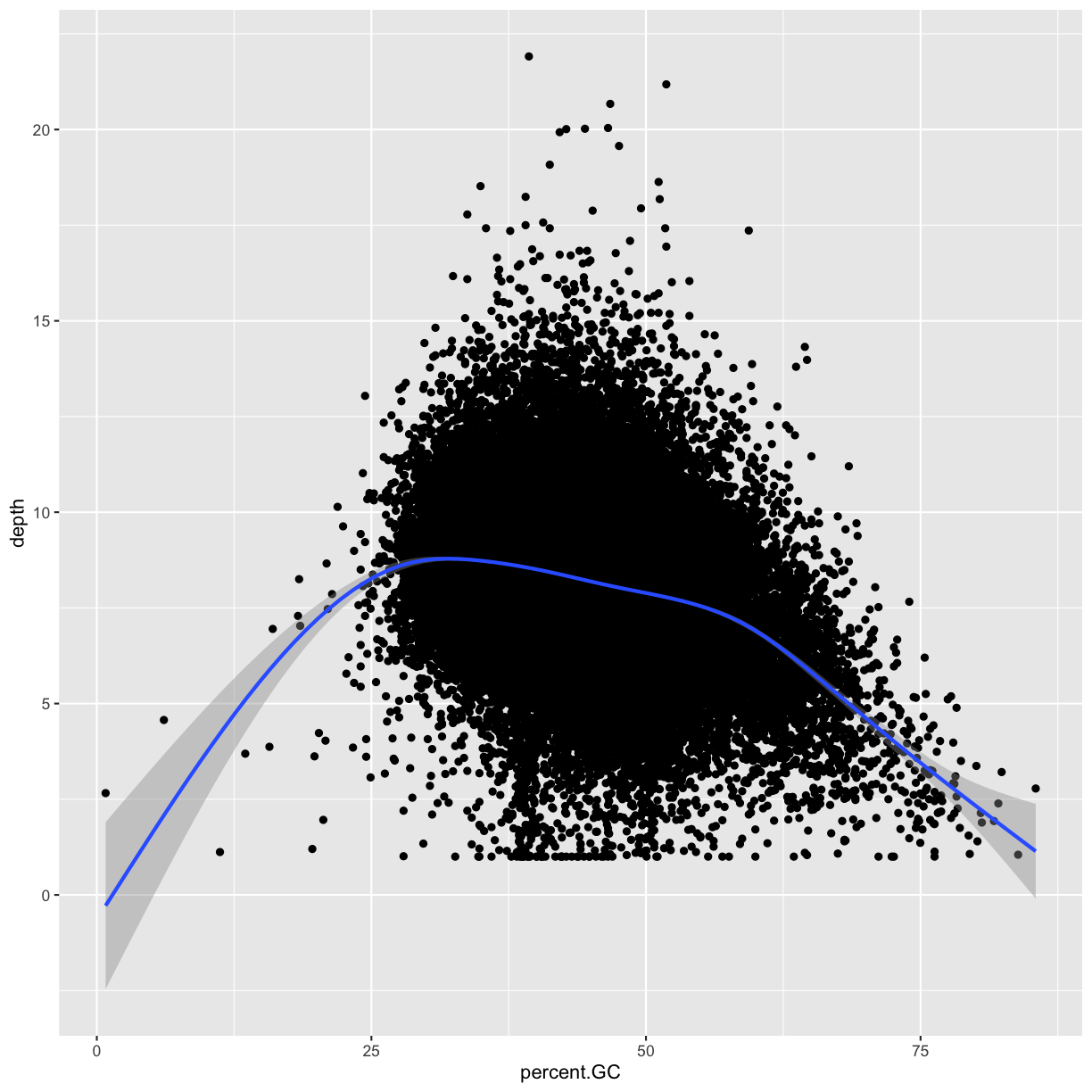
ggplot(data = dvst, mapping = aes(x=depth, y=total.SNPs)) + geom_point(alpha=0.1) + geom_smooth()

`geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'

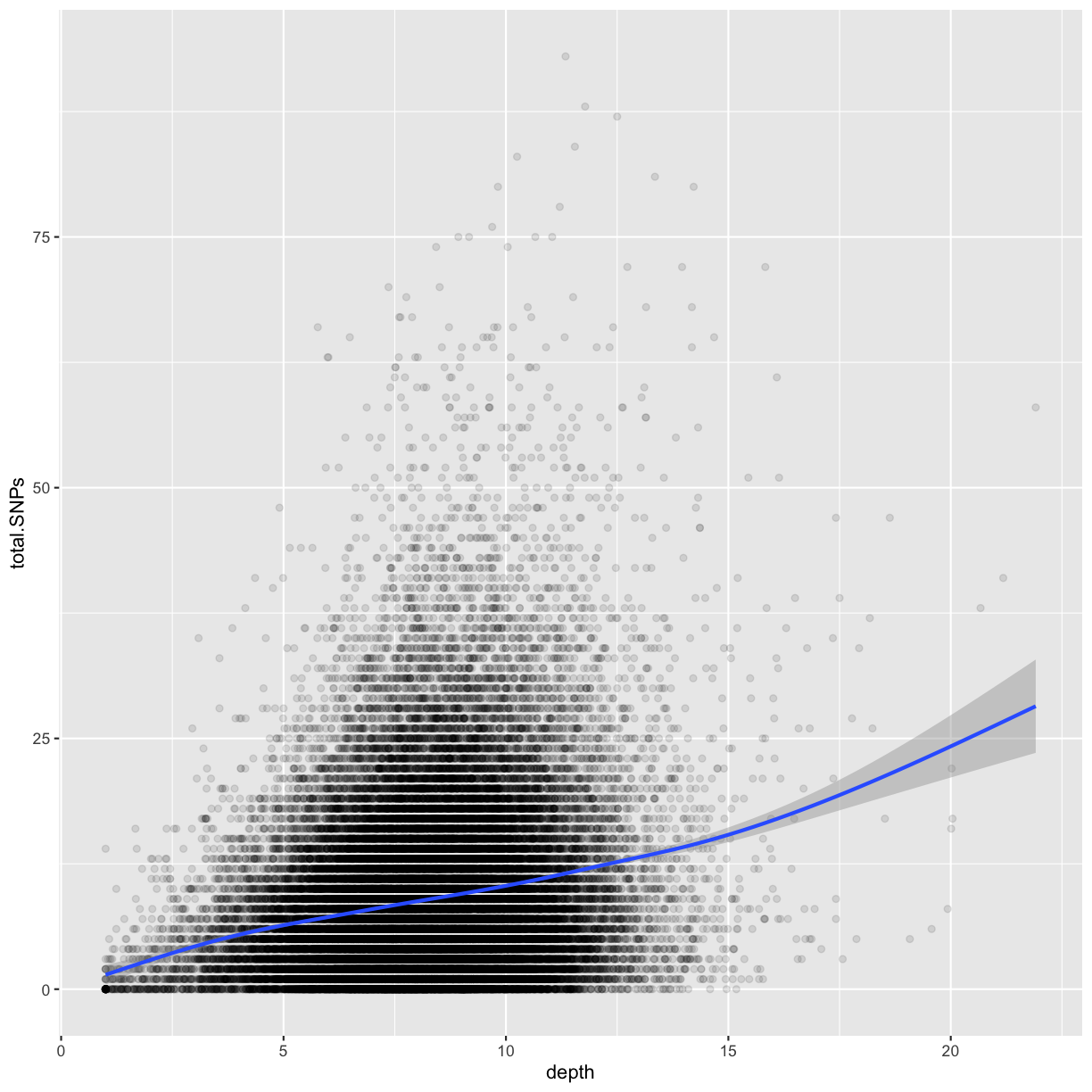
Notice that because both geom_point() and geom_smooth() use the same x and y mapping, we can specify the aesthetic in ggplot() function.

Discussion

1. What does this graph tells us about the relationship between depth of sequencing and SNPs?
2. Why did we put the aesthetic mappings in the call to ggplot()?
3. Try to add the geom_smooth() function to the diversity graphs shown above. Is it more or less informative than using geom_density()? Why?

Challenge 1

Explore the effect GC content has on depth of sequencing in the dataset.

Solution to challenge 1

ggplot(data = dvst, mapping = aes(x=percent.GC, y=depth)) + geom_point() + geom_smooth()

`geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'

Challenge 2

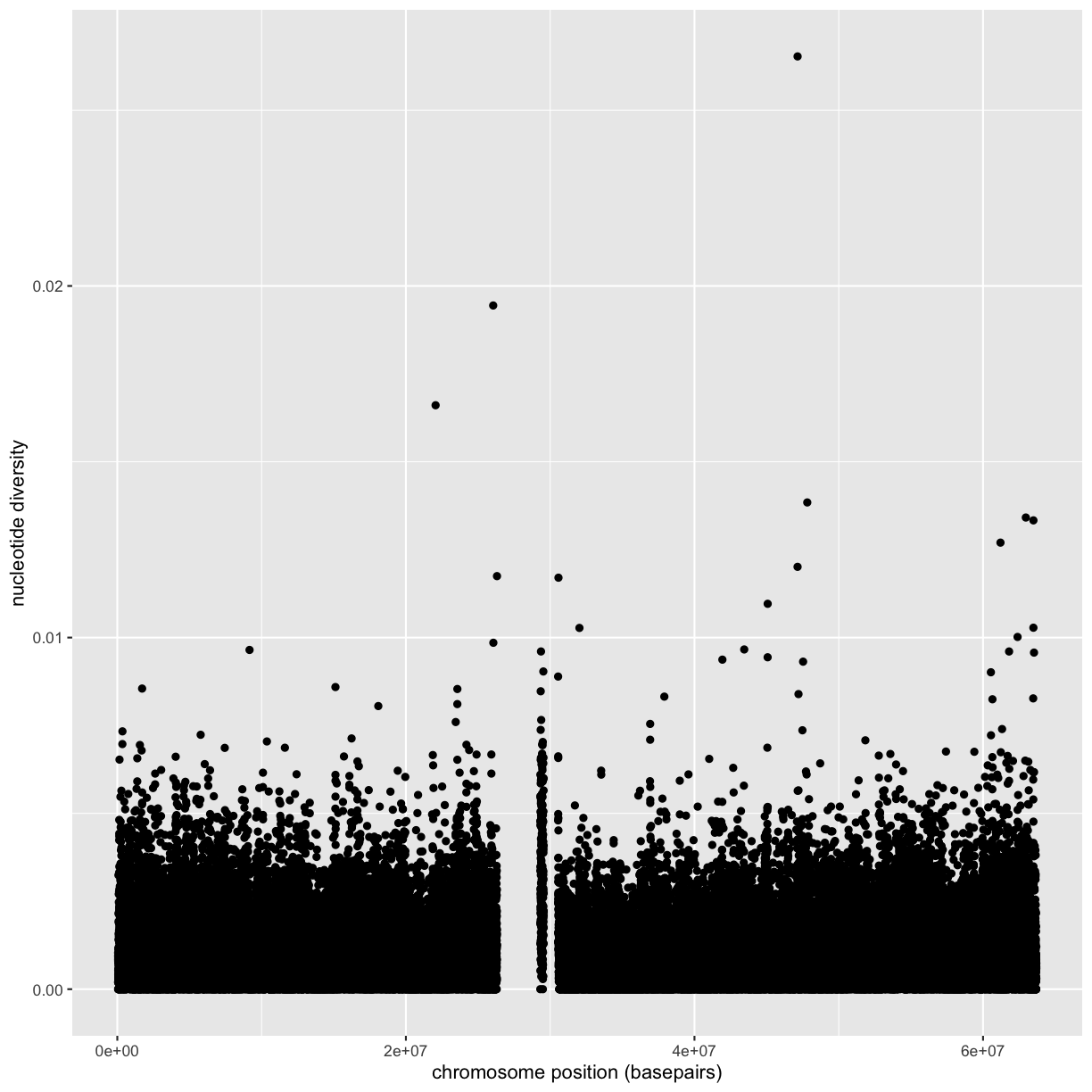
While ggplot2 chooses smart labels based on your column names, you might want to change this down the road. ggplot2 makes specifying labels easy: simply use the xlab(), ylab(), and ggtitle() functions to specify the x-axis label, y-axis label, and plot title. Change x- and y-axis labels when plotting the diversity data with x label “chromosome position (basepairs)” and y label “nucleotide diversity”.

Solution to challenge 2

ggplot(dvst) + geom_point(aes(x=position, y=diversity)) + xlab("chromosome position (basepairs)") + ylab("nucleotide diversity")

Binning Data with cut() and Bar Plots with ggplot2

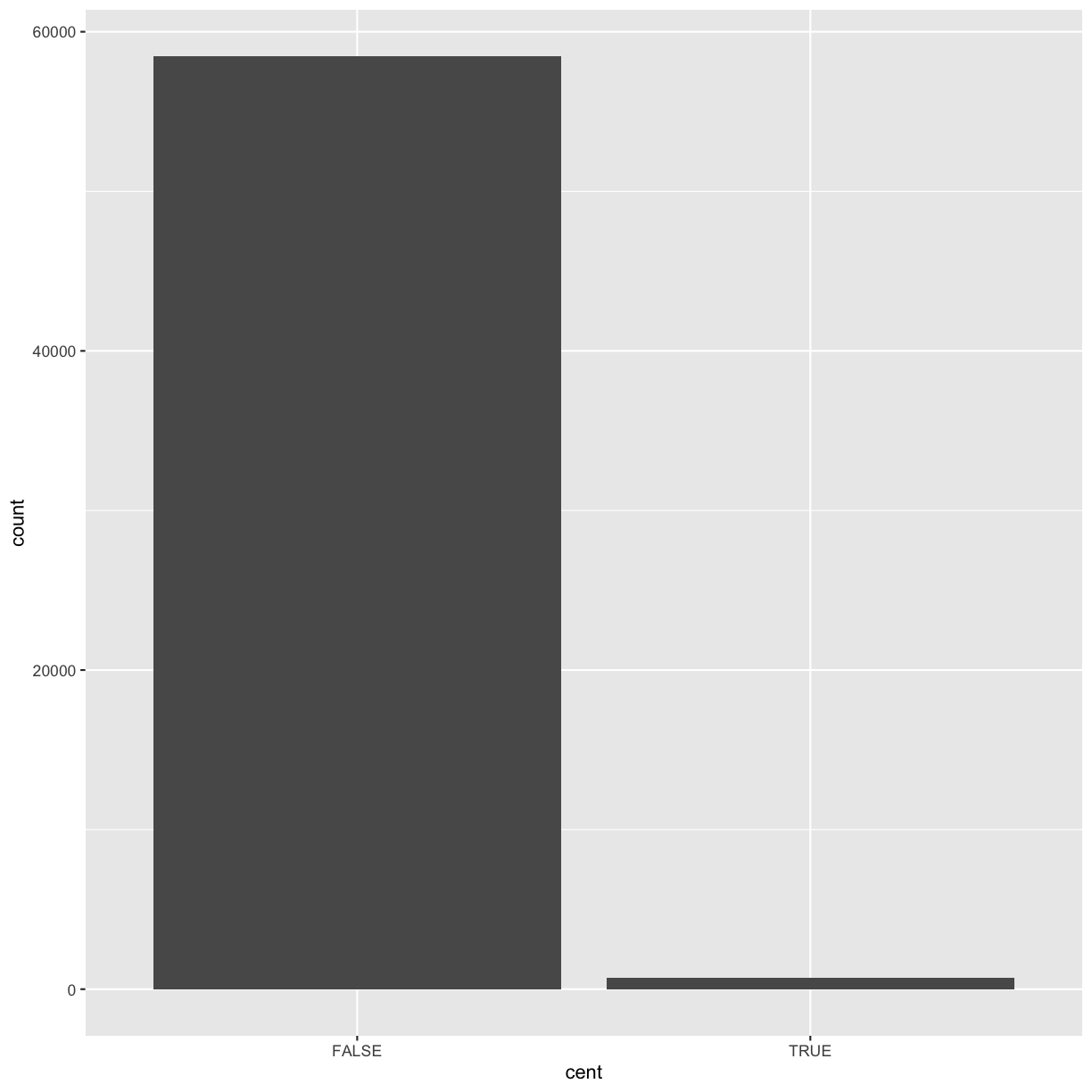
Next, let’s take a look at a bar chart. Bar charts seem simple, but they reveal something subtle about plots. Consider a basic bar chart, as drawn with geom_bar(). As you can see, there are ~60000 windows in the dataset, most of them outside the centromeric region.

ggplot(data = dvst) + 
  geom_bar(mapping = aes(x = cent))

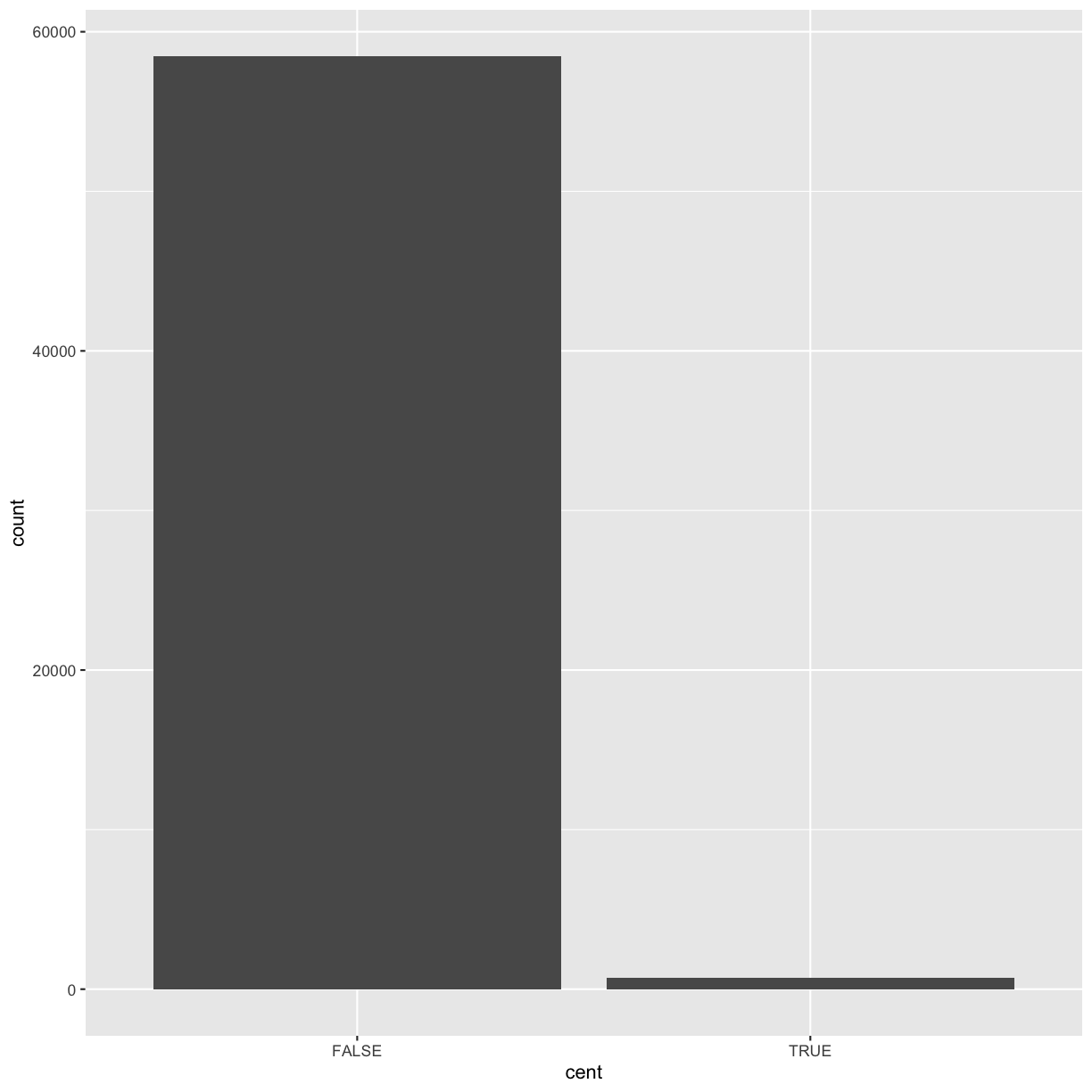
On the x-axis, the chart displays cent, a variable from dvst. On the y-axis, it displays count, but count is not a variable in dvst! Where does count come from? Many graphs, like scatterplots, plot the raw values of your dataset. Other graphs, like bar charts, calculate new values to plot:

• bar charts, histograms, and frequency polygons bin your data and then plot bin counts, the number of points that fall in each bin.

• smoothers fit a model to your data and then plot predictions from the model.

• boxplots compute a robust summary of the distribution and then display a specially formatted box.

The algorithm used to calculate new values for a graph is called a stat, short for statistical transformation. For example, geom_bar() uses stat_count() that simply counts the number of observations.

Extra reading: more about stats

You can learn which stat a geom uses by inspecting the default value for the stat argument. For example, ?geom_bar shows that the default value for stat is “count”, which means that geom_bar() uses stat_count(). stat_count() is documented on the same page as geom_bar(), and if you scroll down you can find a section called “Computed variables”. That describes how it computes two new variables: count and prop.

You can generally use geoms and stats interchangeably. For example, you can recreate the previous plot using stat_count() instead of geom_bar():

ggplot(data = dvst) + 
  stat_count(mapping = aes(x = cent))

This works because every geom has a default stat; and every stat has a default geom. This means that you can typically use geoms without worrying about the underlying statistical transformation. There are three reasons you might need to use a stat explicitly:

1. You might want to override the default stat. For example, the height of the bar may be already present in the data as another variable, in which case you will use stat = "identity"

2. You might want to override the default mapping from transformed variables to aesthetics. For example, you might want to display a bar chart of proportion, rather than count:

   ggplot(data = dvst) + 
     geom_bar(mapping = aes(x = cent, y = ..prop.., group = 1))
   

   

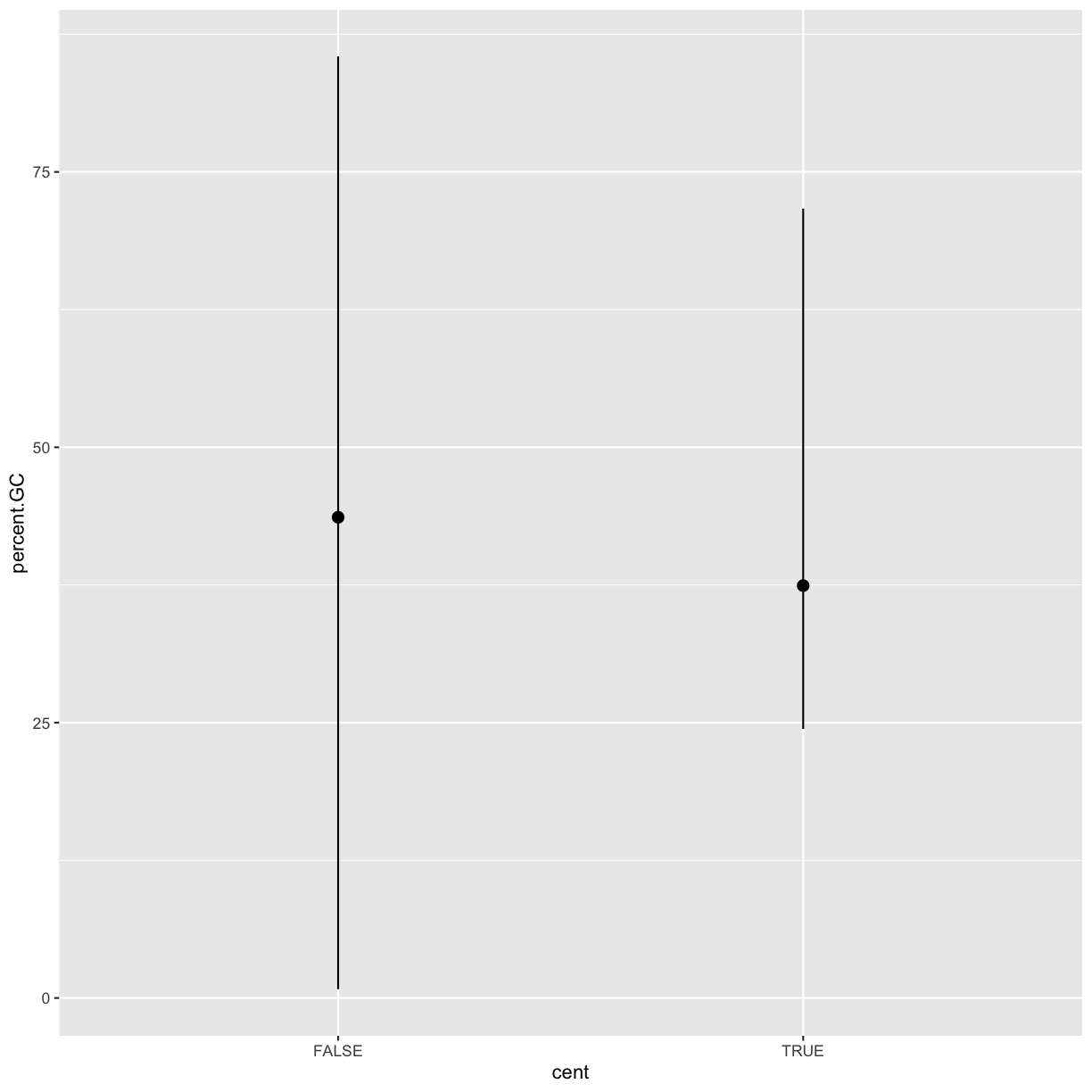
3. You might want to draw greater attention to the statistical transformation in your code. For example, you might use stat_summary(), which summarises the y values for each unique x value, to draw attention to the summary that you’re computing:

   ggplot(data = dvst) + 
     stat_summary(
       mapping = aes(x = cent, y = percent.GC),
       fun.ymin = min,
       fun.ymax = max,
       fun.y = median
     )
   

   Warning: `fun.y` is deprecated. Use `fun` instead.
   

   Warning: `fun.ymin` is deprecated. Use `fun.min` instead.
   

   Warning: `fun.ymax` is deprecated. Use `fun.max` instead.
   

   

ggplot2 provides over 20 stats for you to use. Each stat is a function, so you can get help in the usual way, e.g. ?stat_bin. To see a complete list of stats, check the ggplot2 cheatsheet.

Grouping data

So far we used cent, the only discrete variable in our dataset. Let’s create another one by splitting the percent.GC into 5 categories:

dvst <- dvst %>% 
  mutate(GC.binned = cut(percent.GC, 5));
select(dvst, GC.binned)

# A tibble: 59,140 x 1
   GC.binned  
   <fct>      
 1 (51.6,68.5]
 2 (34.7,51.6]
 3 (34.7,51.6]
 4 (34.7,51.6]
 5 (34.7,51.6]
 6 (34.7,51.6]
 7 (34.7,51.6]
 8 (34.7,51.6]
 9 (34.7,51.6]
10 (17.7,34.7]
# … with 59,130 more rows

ggplot(data = dvst) + geom_bar(mapping = aes(x=GC.binned))

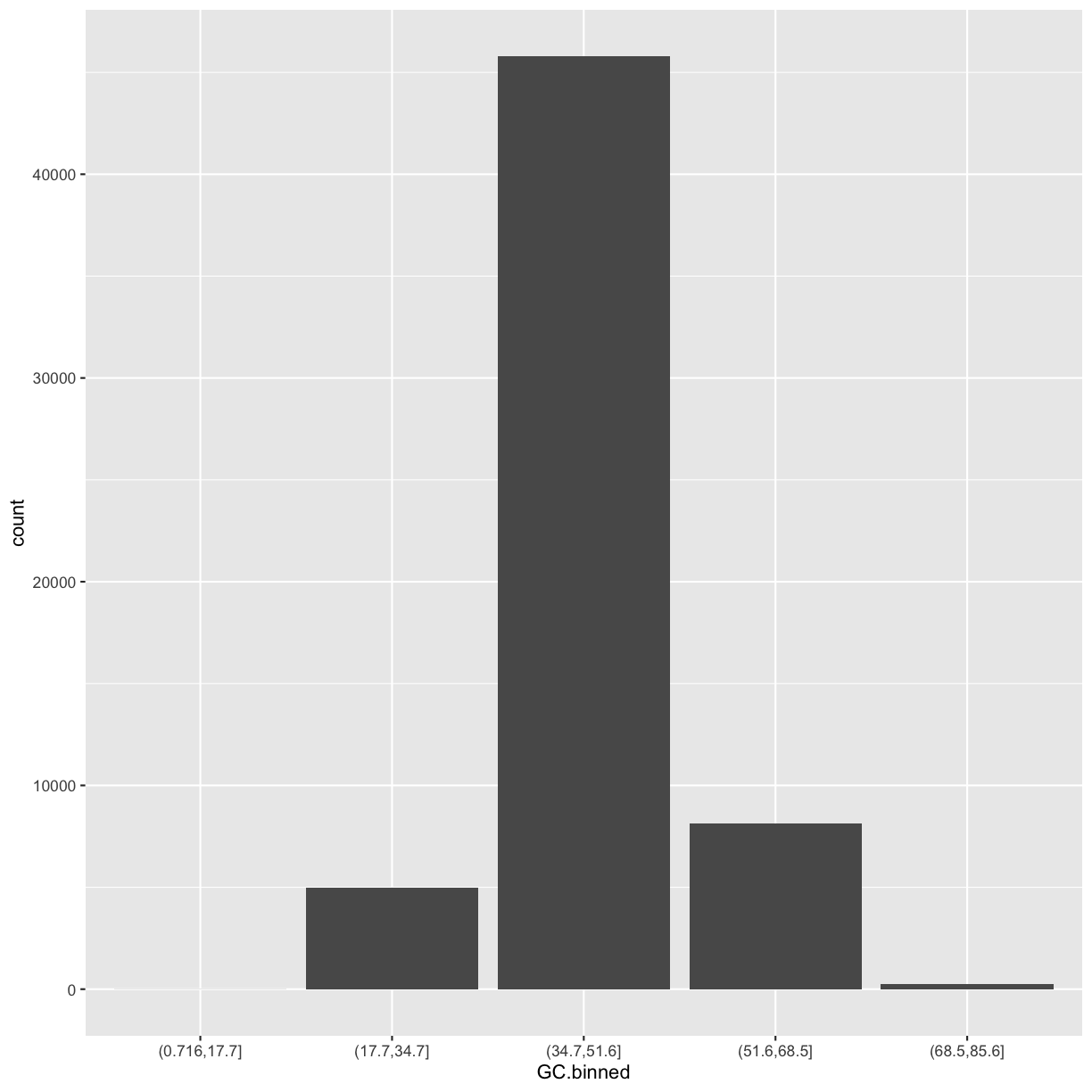
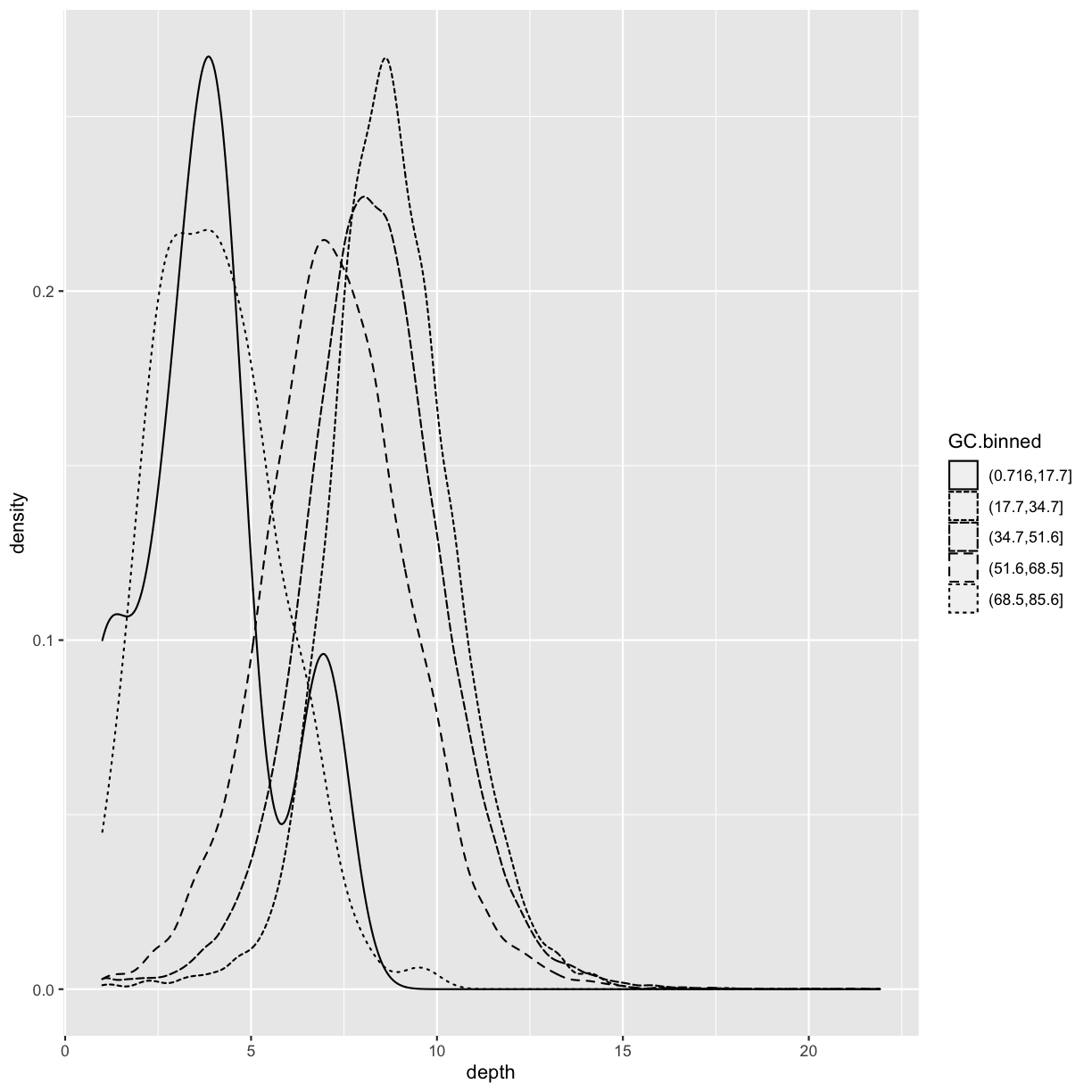
The bins created from cut() are useful in grouping data (a concept we often use in data analysis). For example, we can use the GC.binned column to group data by %GC content bins to see how GC content has an impact on other variables. To do this, we map aesthetics like color, fill, or linetype to our GC.binned column:

ggplot(data = dvst) + geom_density(mapping = aes(x=depth, linetype=GC.binned), alpha=0.5)

What happens if we geom_bar()’s x aesthetic is mapped to a continuous column (e.g., percent.GC)? geom_bar() will automatically bin the data itself, creating a histogram:

ggplot(data = dvst) + geom_bar(mapping = aes(x=percent.GC))

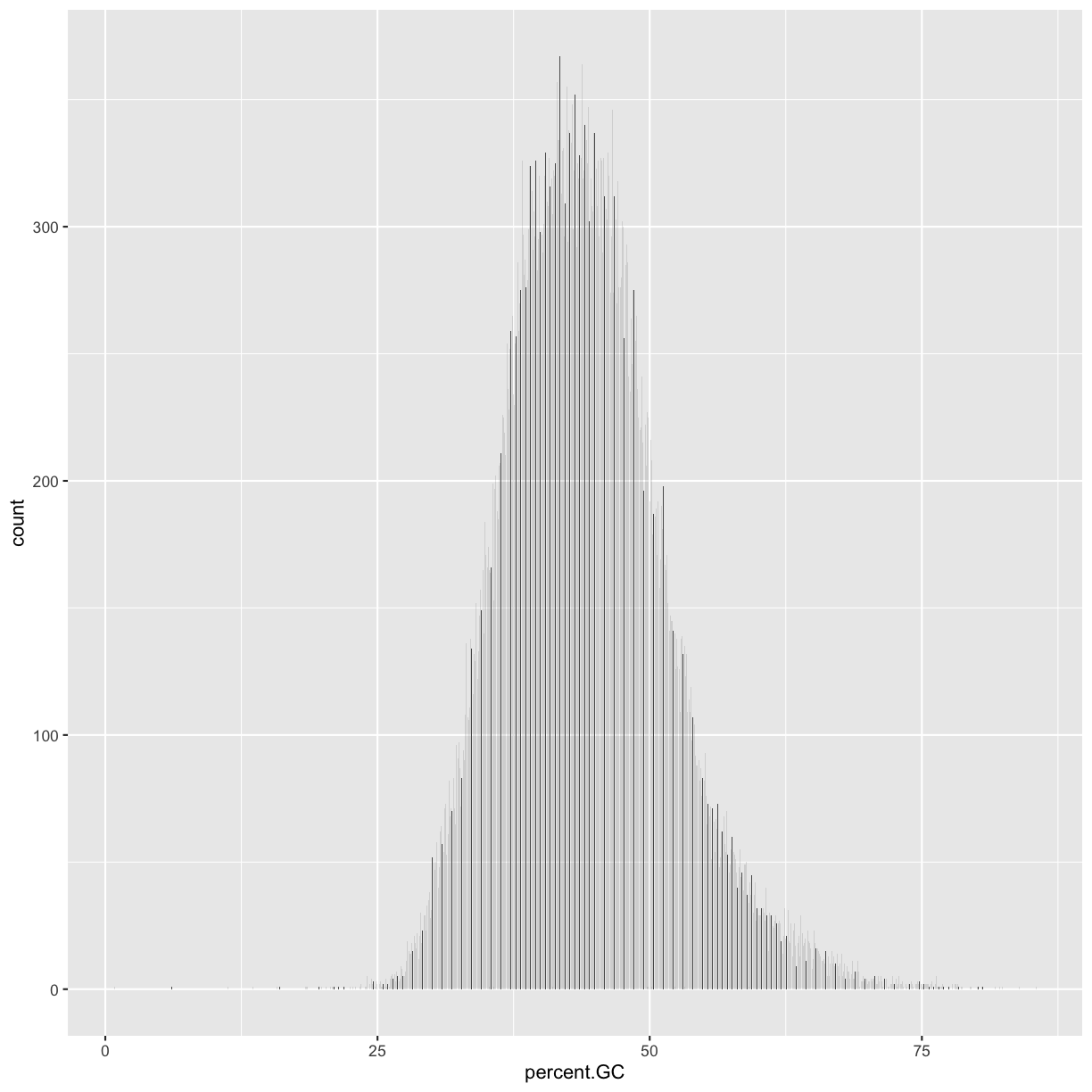
But it does not look like the plot we had! Hence, the challenge:

Challenge 3: Finding the Right Bin Width

We’ve seen before how different bin widths can drastically change the way we view and understand the data. Try creating a histogram of Pi with varying binwidths using: ggplot(dvst) + geom_hist(aes(x=Pi), binwidth=1) + scale_x_continuous(limits=c(0.01, 80)). Using scale_x_continuous() just ignores all windows with 0 Pi and zooms into the figure. Try binwidths of 0.05, 0.5, 1, 5, and 10. What do you observe?

Solution to challenge 3

Smaller bin widths can fit the data better (revealing more subtle details about the distribution), but there’s a trade-off. As bin widths become narrower, each bin will contain fewer data points and consequently be more noisy (and undersmoothed). Using wider bins smooth over this noise. However, bins that are too wide result in oversmoothing, which can hide details about the data.

Position adjustments

There’s one more piece of magic associated with bar charts. You can color a bar chart using either the colour aesthetic, or, more usefully, fill:

ggplot(data = dvst) + 
  geom_bar(mapping = aes(x = GC.binned, colour = GC.binned))

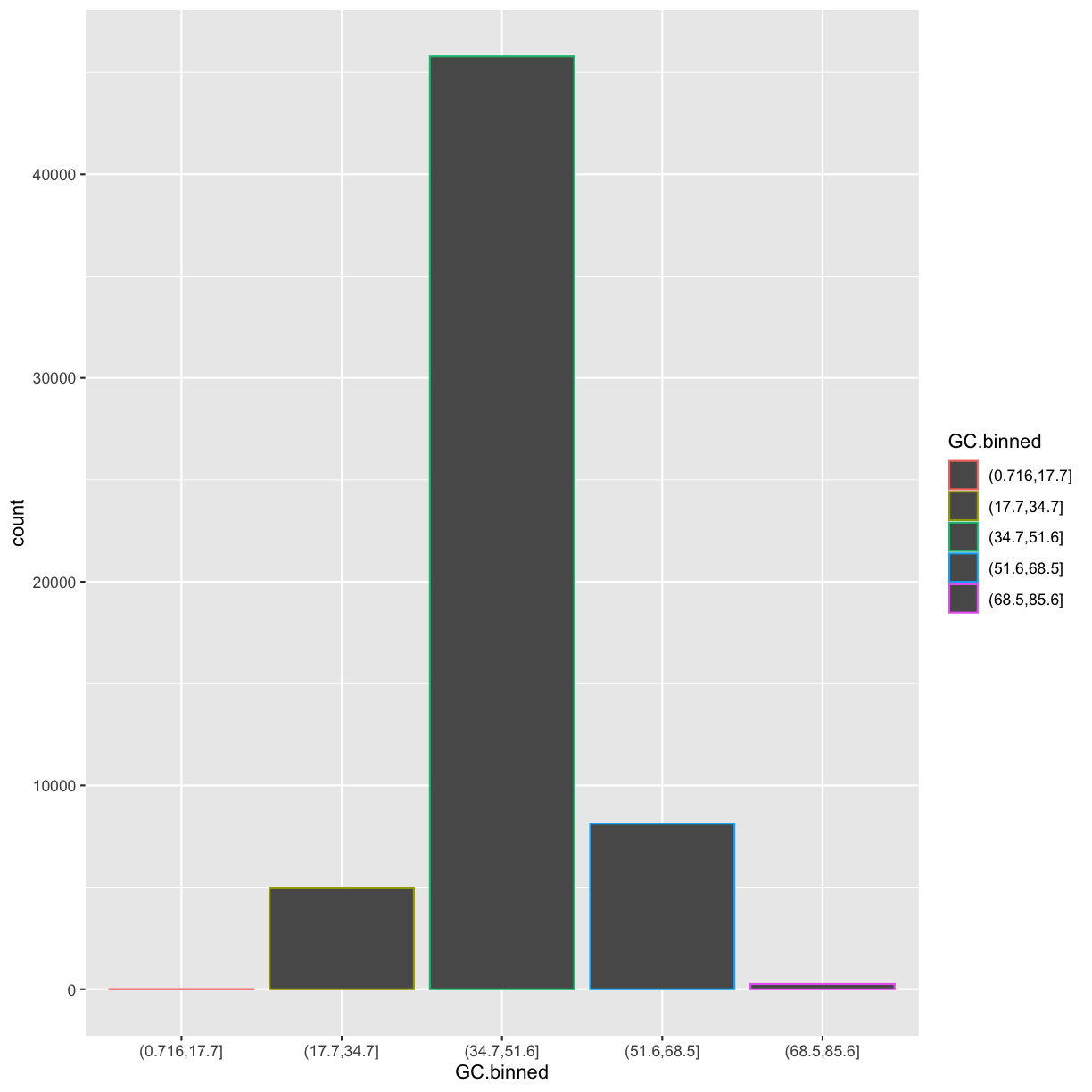
ggplot(data = dvst) + 
  geom_bar(mapping = aes(x = GC.binned, fill = GC.binned))

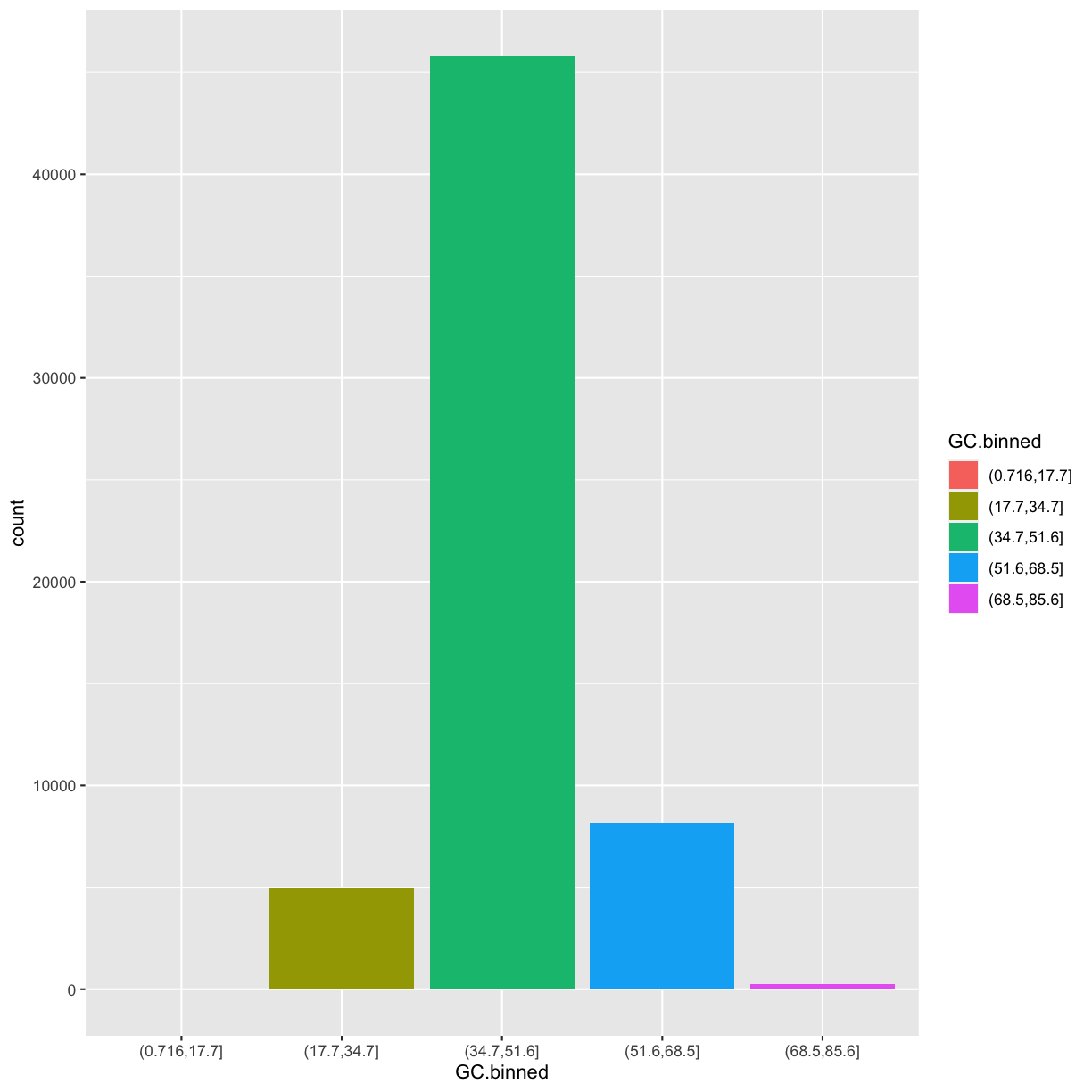
But what happen if you map the fill aesthetic to another variable, like cent? The bars are automatically stacked! Each colored rectangle represents a combination of GC.binned and cent.

ggplot(data = dvst) + 
  geom_bar(mapping = aes(x = GC.binned, fill = cent))

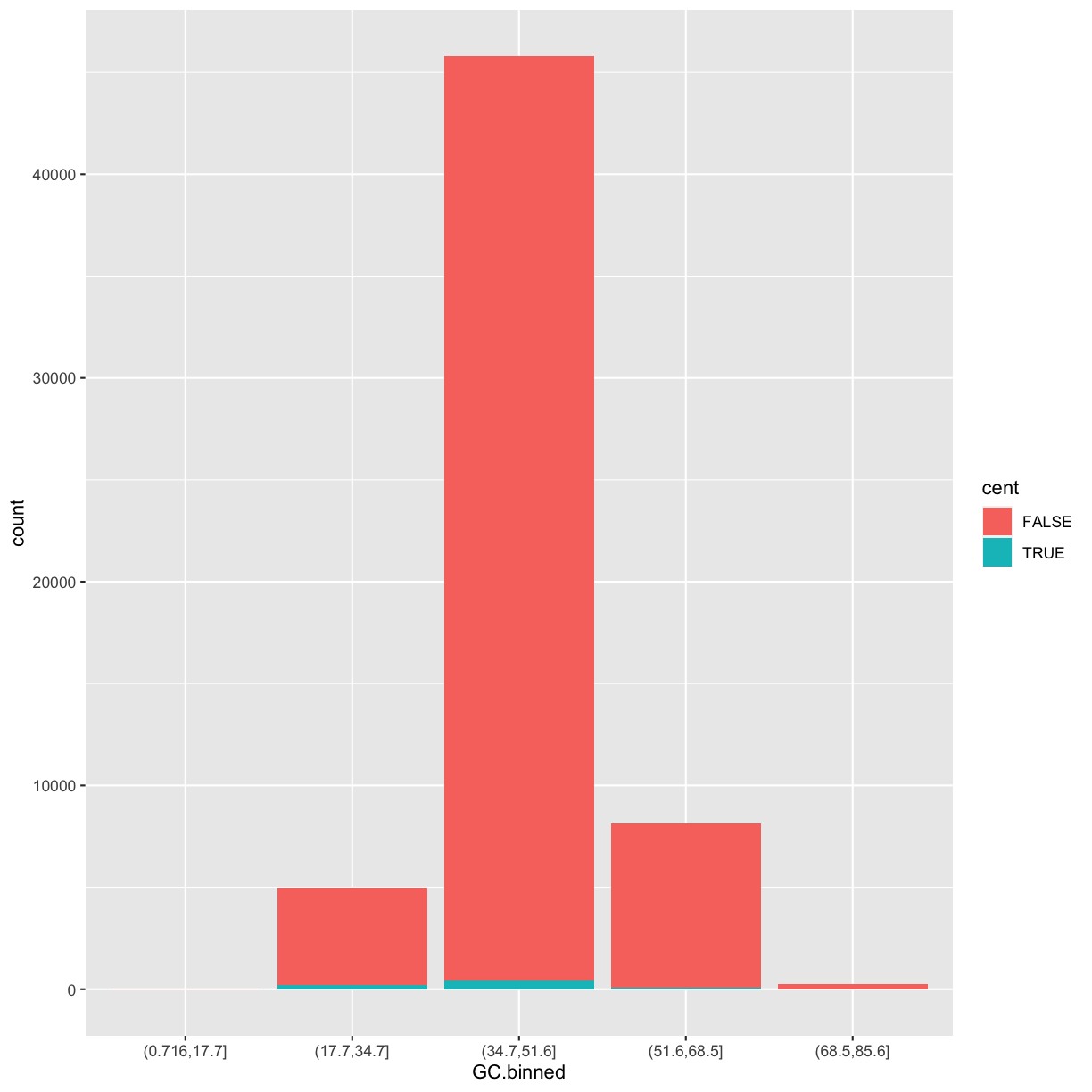
The stacking is performed automatically by the position adjustment specified by the position argument. If you don’t want a stacked bar chart, you can use one of three other options: "identity", "dodge" or "fill".

• position = "identity" will place each object exactly where it falls in the context of the graph. This is not very useful for bars, because it overlaps them. However, the identity position adjustment is more useful for 2d geoms, like points, where it is the default.

• position = "fill" works like stacking, but makes each set of stacked bars the same height. This makes it easier to compare proportions across groups.

  ggplot(data = dvst) + 
    geom_bar(mapping = aes(x = GC.binned, fill = cent), position = "fill")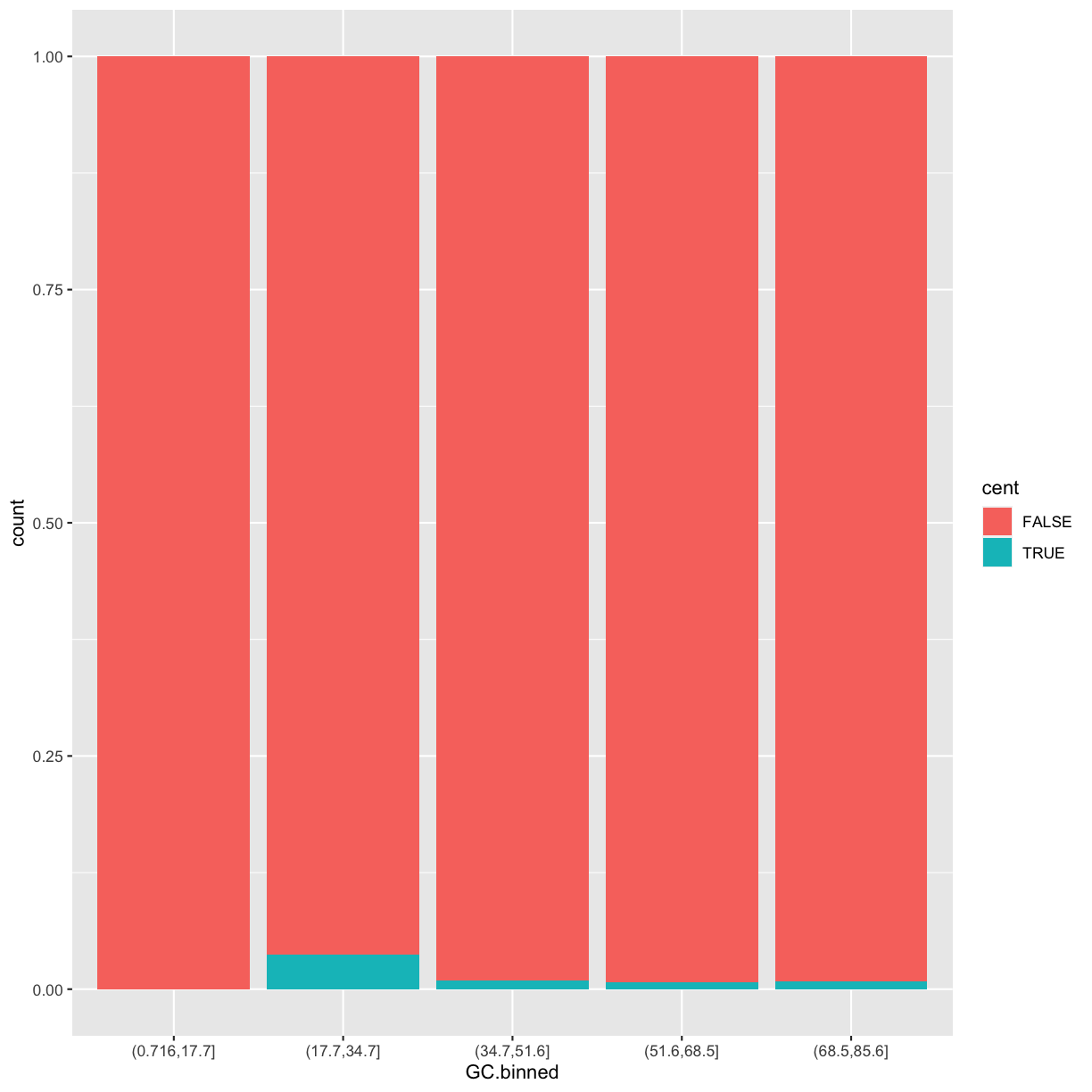
  

  

• position = "dodge" places overlapping objects directly beside one another. This makes it easier to compare individual values.

  ggplot(data = dvst) + 
    geom_bar(mapping = aes(x = GC.binned, fill = cent), position = "dodge")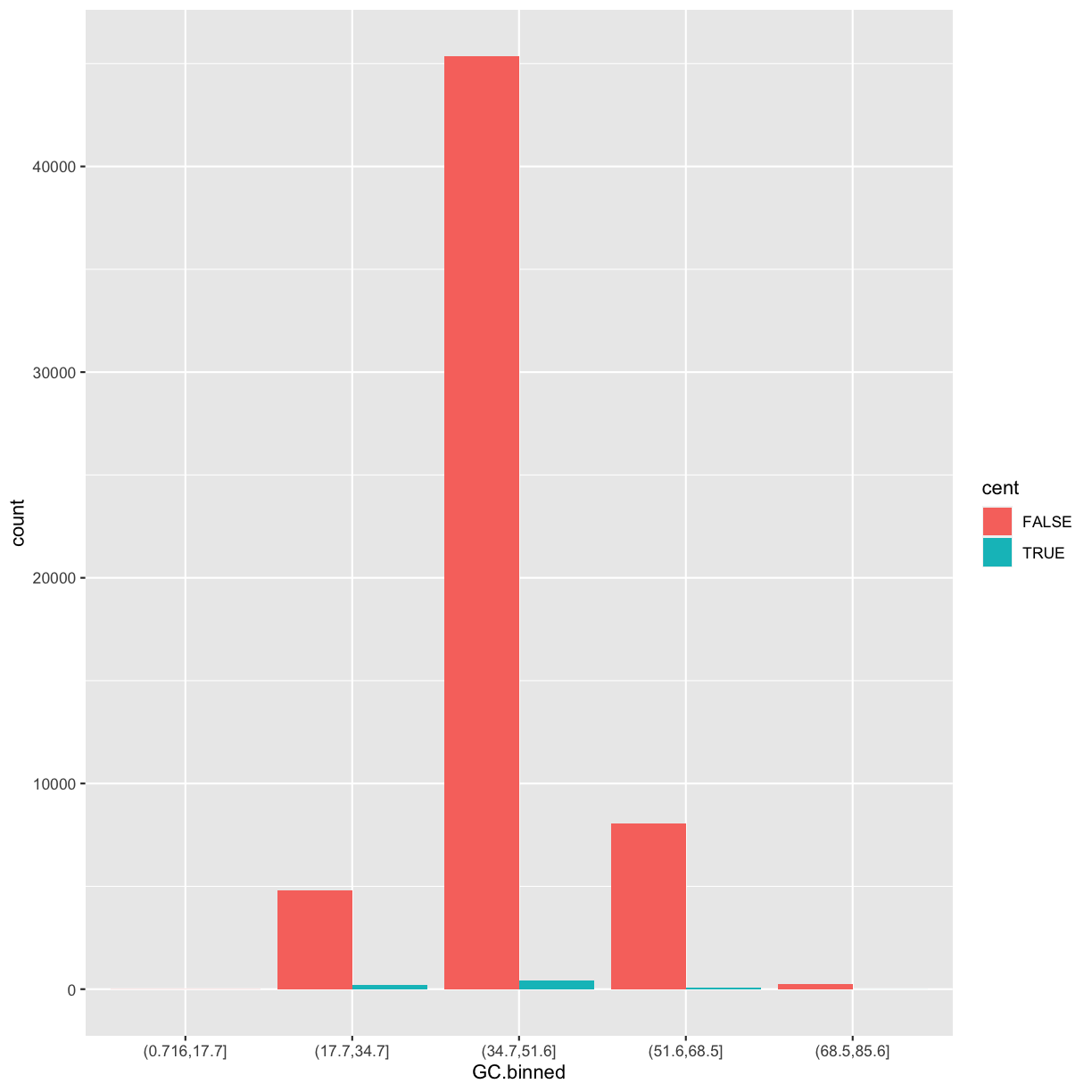
  

  

Dataset #2

Now we’ll return for a minute to data manipulation and create a new tbl by merging two additional datasets available in Buffalo’s bds-files GitHub repository for chapter 8. We start by reading these datasets with read_tsv:

#Read datasets
mtfs <- read_tsv("https://raw.githubusercontent.com/vsbuffalo/bds-files/master/chapter-08-r/motif_recombrates.txt")
rpts <- read_tsv("https://raw.githubusercontent.com/vsbuffalo/bds-files/master/chapter-08-r/motif_repeats.txt")

Here is how they look like:

head(mtfs)

# A tibble: 6 x 9
  chr   motif_start motif_end   dist recomb_start recomb_end  recom motif  pos  
  <chr>       <dbl>     <dbl>  <dbl>        <dbl>      <dbl>  <dbl> <chr>  <chr>
1 chrX     35471312  35471325 39323      35430651   35433340 0.0015 CCTCC… chrX…
2 chrX     35471312  35471325 36977      35433339   35435344 0.0015 CCTCC… chrX…
3 chrX     35471312  35471325 34798.     35435343   35437699 0.0015 CCTCC… chrX…
4 chrX     35471312  35471325 31850.     35437698   35441240 0.0015 CCTCC… chrX…
5 chrX     35471312  35471325 27463      35441239   35446472 0.0015 CCTCC… chrX…
6 chrX     35471312  35471325 24834      35446471   35446498 0.0016 CCTCC… chrX…

head(rpts)

# A tibble: 6 x 5
  chr       start       end name  motif_start
  <chr>     <dbl>     <dbl> <chr>       <dbl>
1 chrX   63005829  63006173 L2       63005830
2 chrX   67746983  67747478 L2       67747232
3 chrX  118646988 118647529 L2      118647199
4 chrX  123998417 123998701 L2      123998675
5 chr13  36171897  36172404 L2       36172069
6 chr13  47030437  47031075 L2       47030836

These two datasets come from a study that explored recombination rates around a degenerate sequence motif that is common in some repeat classes. The first dataset contains estimates of the recombination rate for all windows within 40kb of each of the two motif variants. The second dataset contains info about repeats each motif occur in. Our goal will be to merge these two datasets to look at the effect of specific repeat background on recombination rate.

Using ggplot2 Facets

Here is the plan:

1. combine chr, and motif_start columns in rpts as pos with unite,
2. select this new column along with the name column, and
3. join these two columns with the columns in the mtfs with inner_join. Note, there are several ways you can join to two dataframes.

#Combine columns
rpts2 <- rpts %>% 
  unite(pos, chr, motif_start, sep="-") %>% ## new function!
  select(name, pos) %>% 
  inner_join(mtfs, by="pos")

We will now explore these data using visualization technique known as facets. Facets allow us to visualize grouped data by creating a series of separate adjacent plots for each group. Let’s first glimpse at the relationship between recombination rate and distance to a motif. We’ll construct this graphic in steps:

p <- ggplot(data = rpts2, mapping = aes(x=dist, y=recom)) + geom_point(size=1)
p <- p + geom_smooth(method="loess", se=FALSE, span=1/10)
print(p)

`geom_smooth()` using formula 'y ~ x'

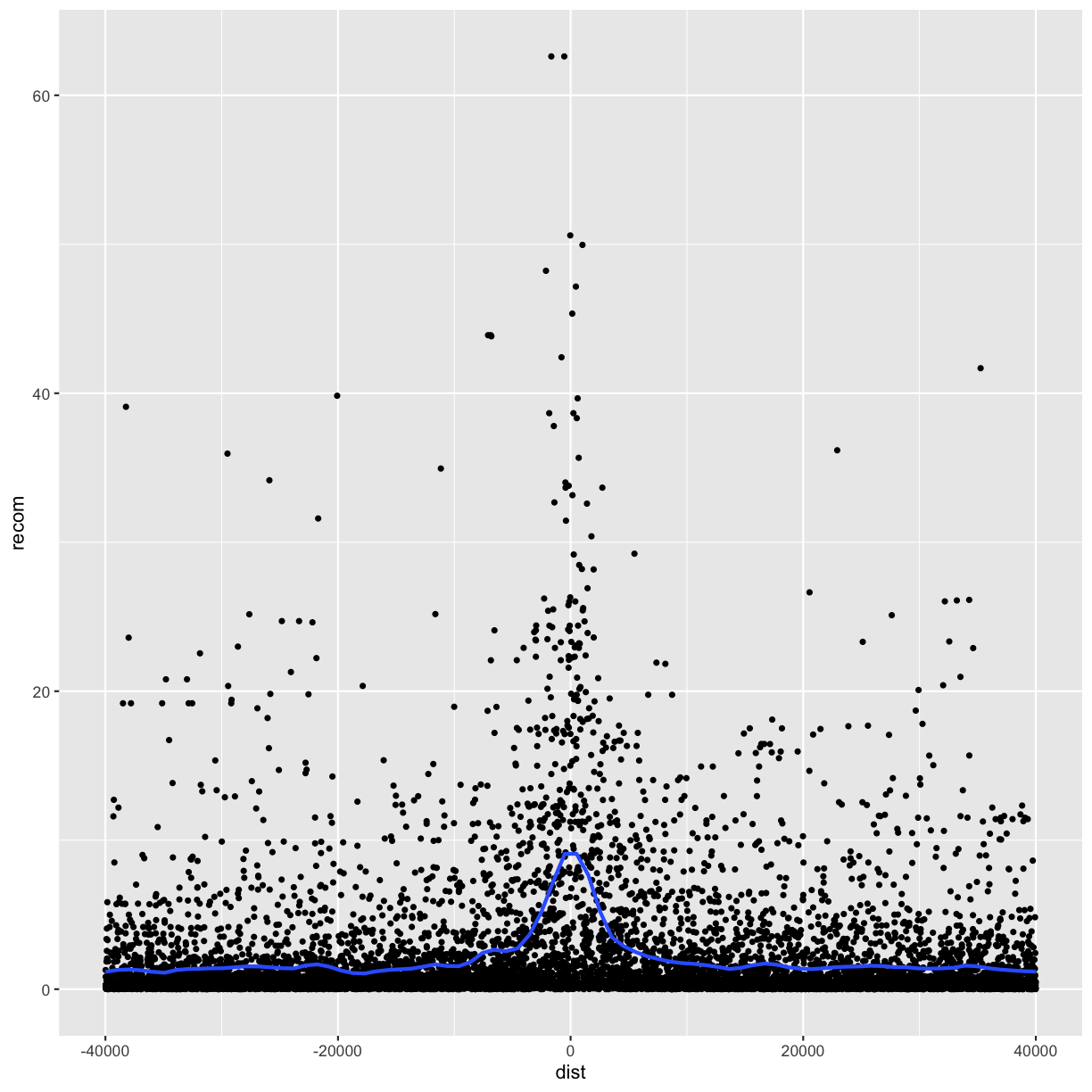
Note that we’ve turned off geom_smooth()’s standard error estimates, adjusted the smoothing with span, and set the smoothing method to “loess”.

From this data, we only see a slight bump in the smoothing curve where the motifs reside. However, this data is a convolution of two different motif sequences on many different genomic backgrounds. In other words, there’s a large amount of heterogeneity we’re not accounting for, and this could be washing out our signal. Let’s use faceting to pick apart this data.

First, if you’ve explored the rpts dataframe, you’ll notice that the motif column contains two variations of the sequence motif:

distinct(rpts2, motif)

# A tibble: 2 x 1
  motif        
  <chr>        
1 CCTCCCTGACCAC
2 CCTCCCTAGCCAC

One way to compare these is by grouping and coloring the loess curves by motif sequence:

ggplot(data = rpts2, mapping = aes(x=dist, y=recom)) + geom_point(size=1) + 
  geom_smooth(aes(color=motif), method="loess", se=FALSE, span=1/10)

`geom_smooth()` using formula 'y ~ x'

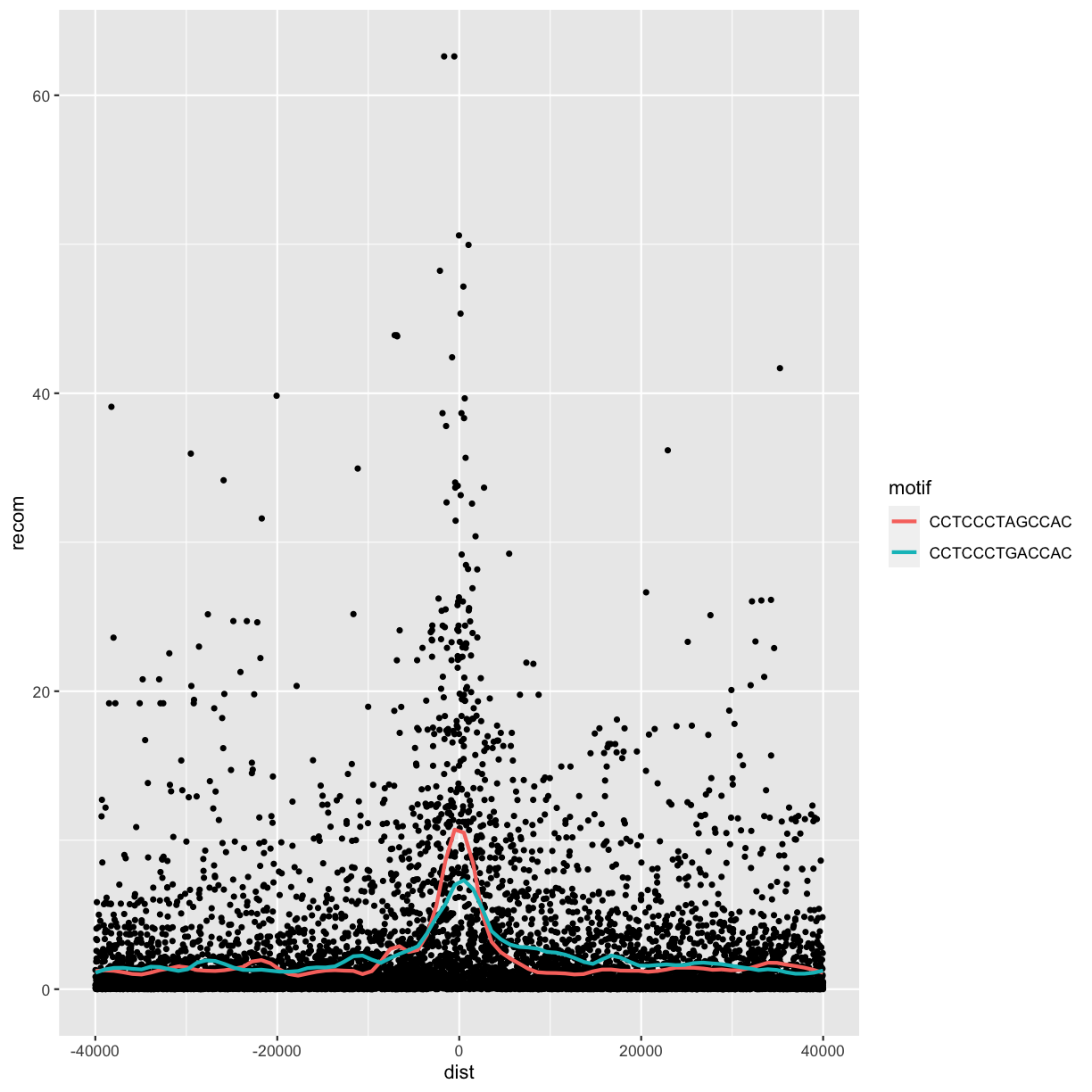
Alternatively, we can split these motifs apart visually with facets using ggplot2’s facet_wrap() or facet_grid().

Facet_wrap()

To facet your plot by a single variable, use facet_wrap(). facet_wrap() takes a factor column, creates a panel for each level and wraps around horizontally. The first argument of facet_wrap() should be a formula, which you create with ~ followed by a variable name.

p <- ggplot(data = rpts2, mapping = aes(x=dist, y=recom)) + geom_point(size=1, color="grey")
p <- p + geom_smooth(method='loess', se=FALSE, span=1/10)
p <- p + facet_wrap(~ motif)
print(p)

`geom_smooth()` using formula 'y ~ x'

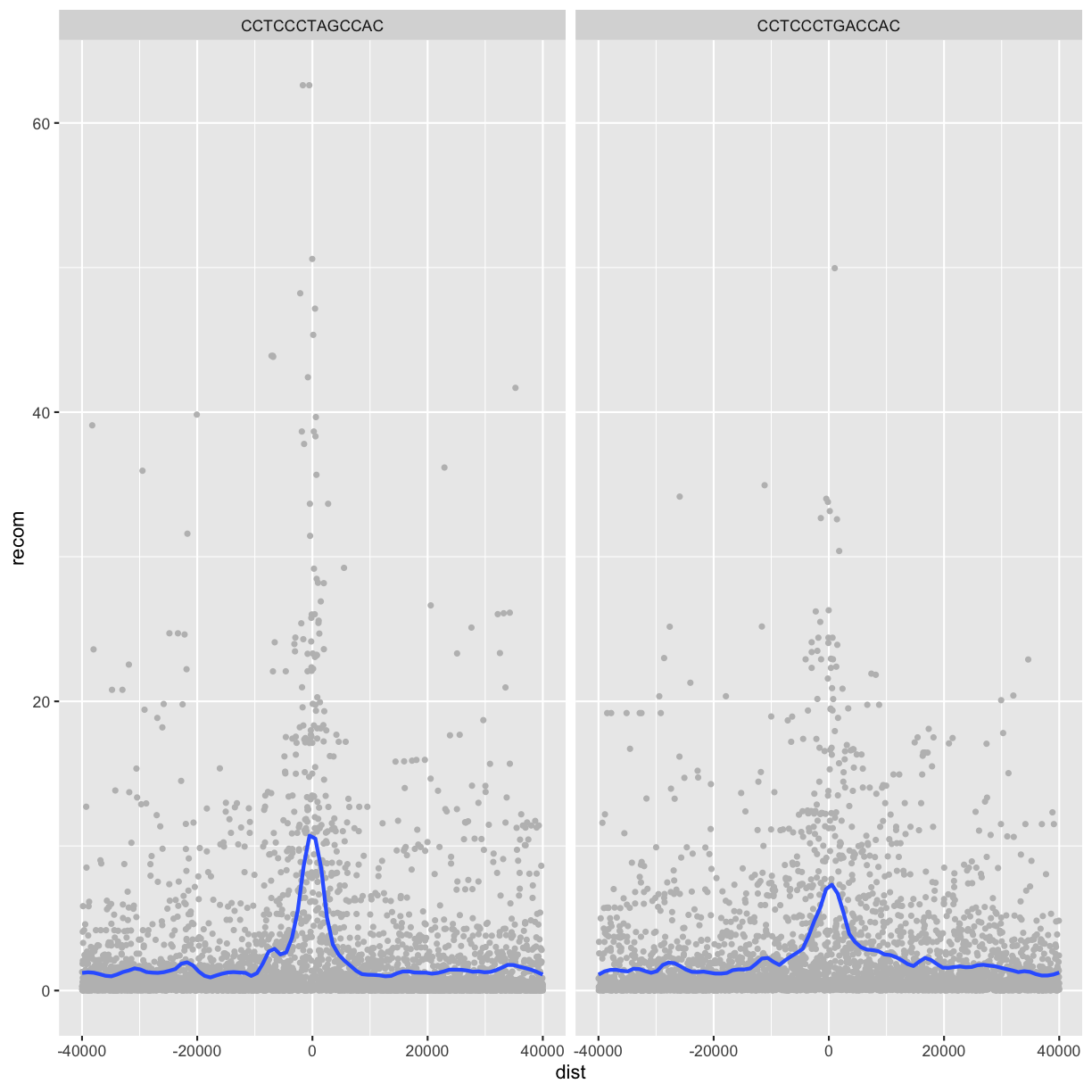
Facet_grid()

To facet your plot on the combination of two variables, add facet_grid() to your plot call. The first argument of facet_grid() is also a formula. This time the formula should contain two variable names separated by a ~.

If you prefer to not facet in the rows or columns dimension, use a . instead of a variable name, e.g. + facet_grid(. ~ motif).

rpts

# A tibble: 317 x 5
   chr       start       end name  motif_start
   <chr>     <dbl>     <dbl> <chr>       <dbl>
 1 chrX   63005829  63006173 L2       63005830
 2 chrX   67746983  67747478 L2       67747232
 3 chrX  118646988 118647529 L2      118647199
 4 chrX  123998417 123998701 L2      123998675
 5 chr13  36171897  36172404 L2       36172069
 6 chr13  47030437  47031075 L2       47030836
 7 chr13 112828064 112828466 L2      112828268
 8 chr12  44799399  44799664 L2       44799602
 9 chr12  71407097  71407379 L2       71407292
10 chr12 102646349 102646646 L2      102646586
# … with 307 more rows

p <- ggplot(rpts2, aes(x=dist, y=recom)) + geom_point(size=1, color="grey")
p <- p + geom_smooth(method='loess', se=FALSE, span=1/16)
p <- p + facet_grid(name ~ motif)
print(p)

`geom_smooth()` using formula 'y ~ x'

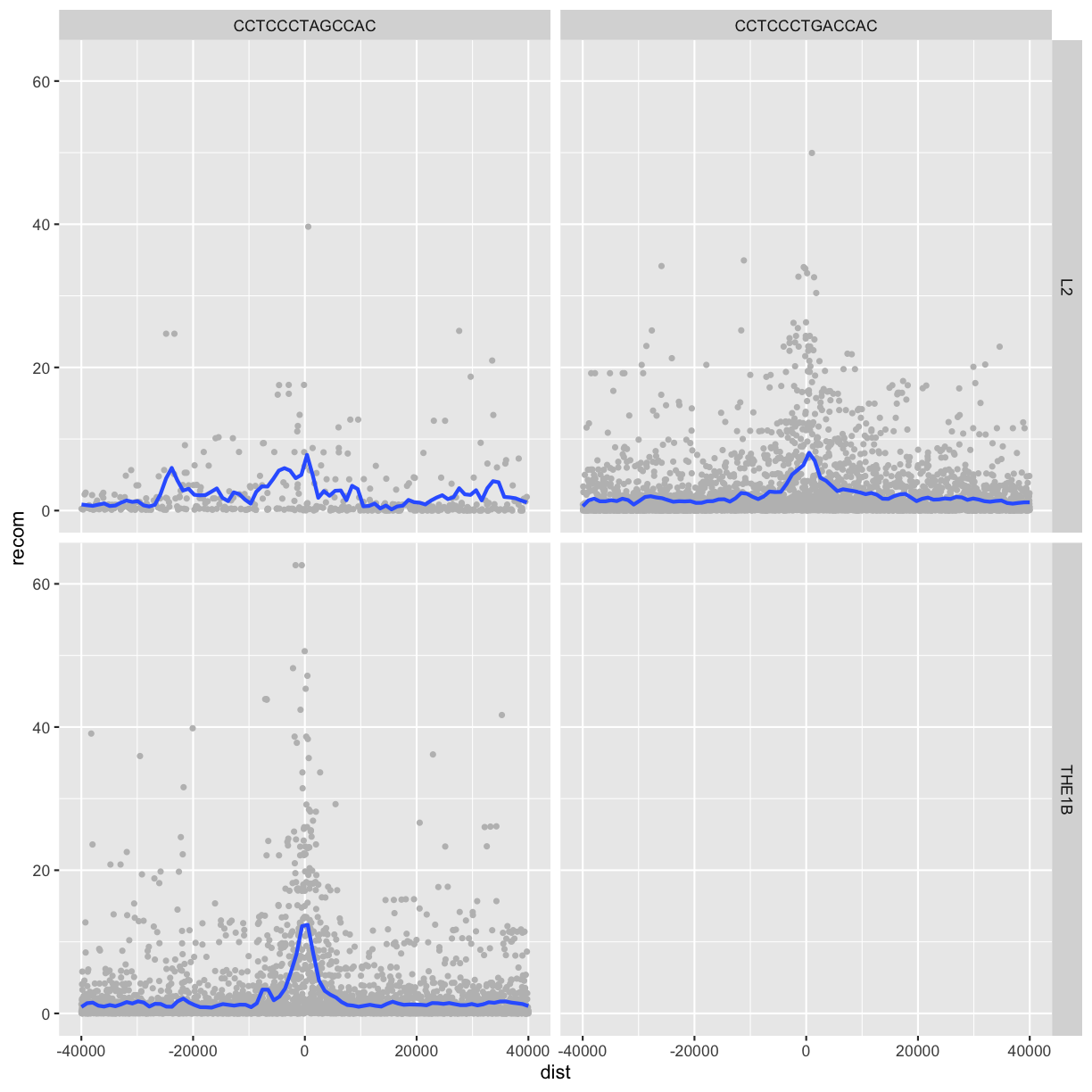
We see some patterns emerging here: motif CCTCCCTAGCCAC on a THE1B repeat background has a strong effect on recombination rate, as does CCTCCCTGACCAC on a L2 repeat background. You can get a sense of the data that goes into this plot with:

table(rpts2$name, rpts2$motif, useNA="ifany")

       
        CCTCCCTAGCCAC CCTCCCTGACCAC
  L2              457          4110
  THE1B          4651             0

rpts2 %>% 
  count(name, motif)

# A tibble: 3 x 3
  name  motif             n
  <chr> <chr>         <int>
1 L2    CCTCCCTAGCCAC   457
2 L2    CCTCCCTGACCAC  4110
3 THE1B CCTCCCTAGCCAC  4651

One important feature of facet_wrap() and facet_grid() is that by default, x- and y-scales will be the same across all panels. You can set scales to be free with scales=”free_x” and scales=”free_y”, or scales=”free” to free both axes.

For example:

p <- ggplot(rpts2, aes(x=dist, y=recom)) + geom_point(size=1, color="grey")
p <- p + geom_smooth(method='loess', se=FALSE, span=1/10)
p <- p + facet_wrap( ~ motif, scales="free_y")
print(p)

`geom_smooth()` using formula 'y ~ x'

Challenge 4: Recombination rate by chromosome

Try using facets to look at this data when grouped by chromosome with facet_wrap( ~ chr).

Extra reading: coordinate systems

Coordinate systems are probably the most complicated part of ggplot2. The default coordinate system is the Cartesian coordinate system where the x and y positions act independently to determine the location of each point. There are a number of other coordinate systems that are occasionally helpful.

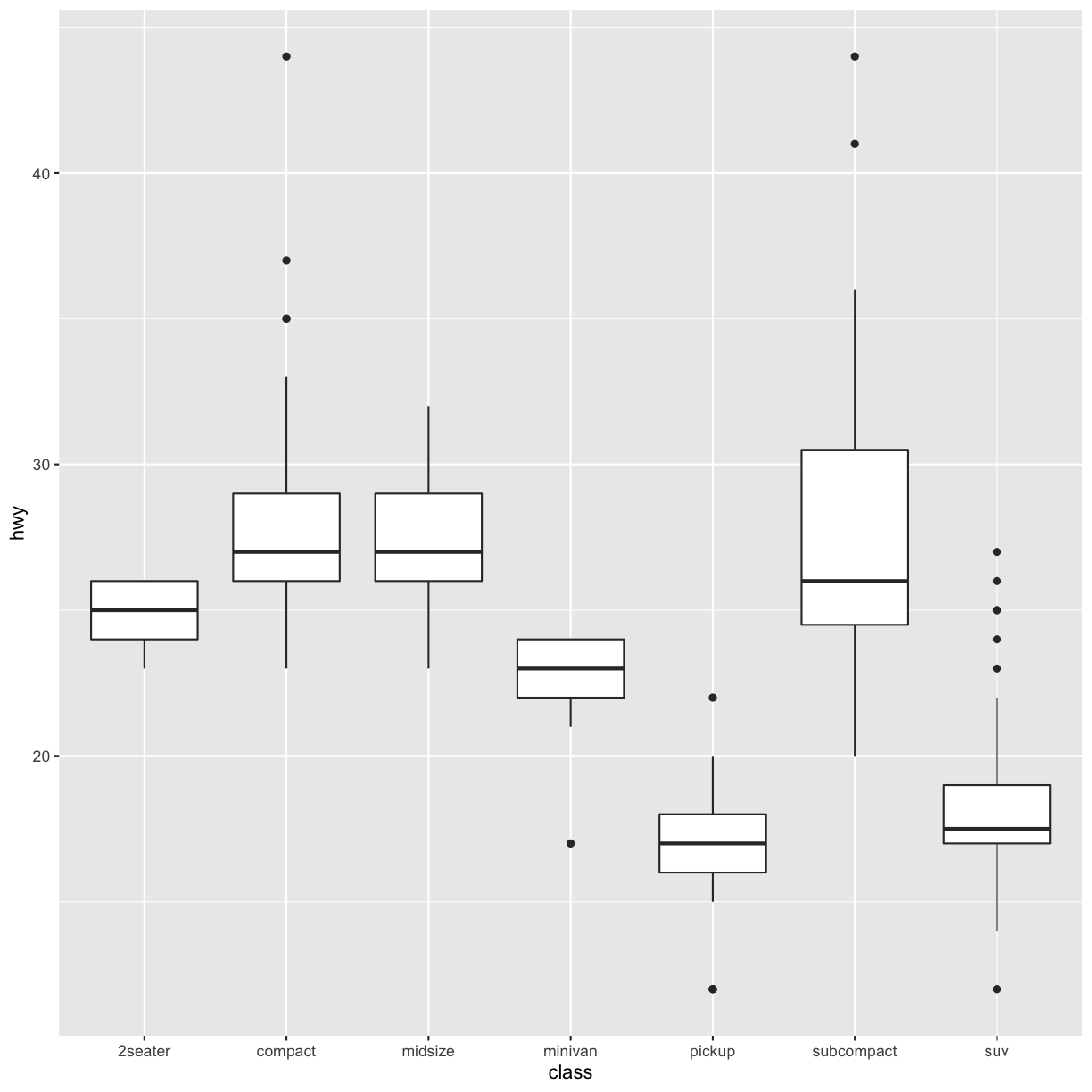
• coord_flip() switches the x and y axes. This is useful (for example), if you want horizontal boxplots. It’s also useful for long labels: it’s hard to get them to fit without overlapping on the x-axis.

  #fig.width = 3, out.width = "50%", fig.align = "default"}
  ggplot(data = mpg, mapping = aes(x = class, y = hwy)) + 
    geom_boxplot()
  

  

  ggplot(data = mpg, mapping = aes(x = class, y = hwy)) + 
    geom_boxplot() +
    coord_flip()
  

  

• coord_quickmap() sets the aspect ratio correctly for maps. This is very important if you’re plotting spatial data with ggplot2.

  #fig.width = 3, out.width = "50%", fig.align = "default", message = FALSE}
  nz <- map_data("nz")
  

  Error:   Package `maps` required for `map_data`.
    Please install and try again.
  

  ggplot(nz, aes(long, lat, group = group)) +
    geom_polygon(fill = "white", colour = "black")
  

  Error in ggplot(nz, aes(long, lat, group = group)): object 'nz' not found
  

  ggplot(nz, aes(long, lat, group = group)) +
    geom_polygon(fill = "white", colour = "black") +
    coord_quickmap()
  

  Error in ggplot(nz, aes(long, lat, group = group)): object 'nz' not found
  

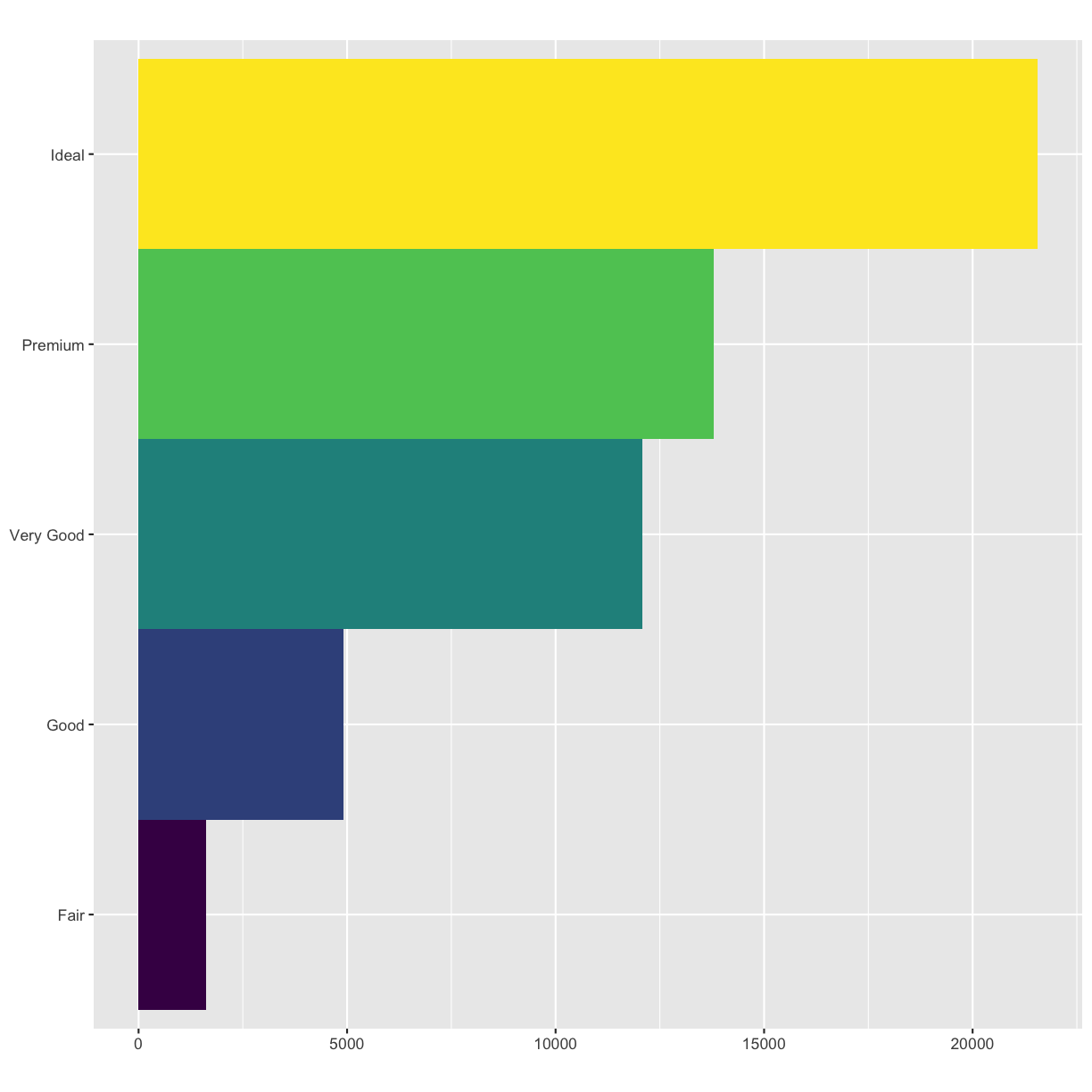
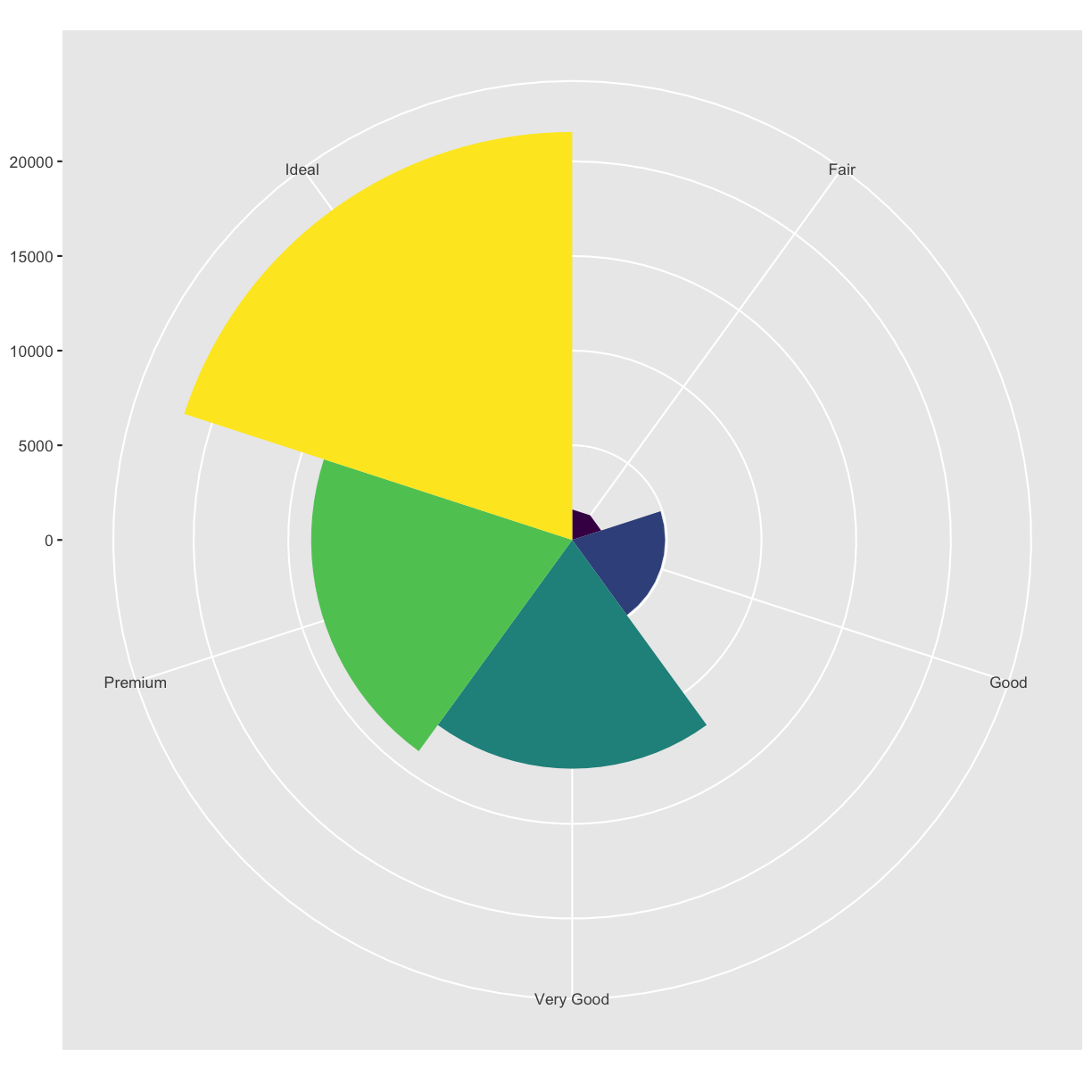
• coord_polar() uses polar coordinates. Polar coordinates reveal an interesting connection between a bar chart and a Coxcomb chart.

  #fig.width = 3, out.width = "50%", fig.align = "default", fig.asp = 1}
  bar <- ggplot(data = diamonds) + 
    geom_bar(
      mapping = aes(x = cut, fill = cut), 
      show.legend = FALSE,
      width = 1
    ) + 
    theme(aspect.ratio = 1) +
    labs(x = NULL, y = NULL)
      
  bar + coord_flip()
  

  

  bar + coord_polar()
  

  

Saving the plot

ggsave() is a convenient function for saving a plot. It defaults to saving the last plot that you displayed, using the size of the current graphics device. It also guesses the type of graphics device from the extension.

ggsave("myplot.pdf")
ggsave("myplot.png")

The layered grammar of graphics

In the previous sections, you learned much more than how to make scatterplots, bar charts, and boxplots. You learned a foundation that you can use to make any type of plot with ggplot2. To see this, let’s add position adjustments, stats, coordinate systems, and faceting to our code template:

ggplot(data = <DATA>) + 
  <GEOM_FUNCTION>(
     mapping = aes(<MAPPINGS>),
     stat = <STAT>, 
     position = <POSITION>
  ) +
  <COORDINATE_FUNCTION> +
  <FACET_FUNCTION>

Our new template takes seven parameters, the bracketed words that appear in the template. In practice, you rarely need to supply all seven parameters to make a graph because ggplot2 will provide useful defaults for everything except the data, the mappings, and the geom function.

The seven parameters in the template compose the grammar of graphics, a formal system for building plots. The grammar of graphics is based on the insight that you can uniquely describe any plot as a combination of a dataset, a geom, a set of mappings, a stat, a position adjustment, a coordinate system, and a faceting scheme.

You could use this method to build any plot that you imagine. In other words, you can use the code template that you’ve learned in this chapter to build hundreds of thousands of unique plots.

ggplot2 calls

So far we’ve been very explicit with ggplot2 code:

ggplot(data = faithful, mapping = aes(x = eruptions)) + 
  geom_freqpoly(binwidth = 0.25)

Typically, the first one or two arguments to a function are so important that you should know them by heart. The first two arguments to ggplot() are data and mapping, and the first two arguments to aes() are x and y. And if you know them by heart, you don’t need to type them! That makes it easier to see what’s different between plots. Rewriting the previous plot more concisely yields:

ggplot(faithful, aes(eruptions)) + 
  geom_freqpoly(binwidth = 0.25)

Sometimes we’ll turn the end of a pipeline of data transformation into a plot. Watch for the transition from %>% to +. This transition is necessary because ggplot2 was created before the pipe was discovered.

Key Points

• Use ggplot2 to create plots.

• Think about graphics in layers: aesthetics, geometry, statistics, scale transformation, and grouping.